题目内容
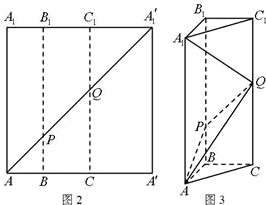 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.(1)在三棱柱ABC-A1B1C1中,求证:AB⊥平面BCC1B1.
(2)求平面APQ将三棱柱ABC-A1B1C1分成上、下两部分几何体的体积之比.
(3)在三棱柱ABC-A1B1C1中,求直线AP与直线A1Q所成角的余弦值.
分析:(1)在三棱柱ABC-A1B1C1中,证明AB垂直平面BCC1B1内的两条相交直线BC、BB1即可.
(2)说明AB为四棱锥A-BCQP的高,求出梯形BCQP的面积,即可求出平面APQ将三棱柱ABC-A1B1C1分成上部分的体积;同理求出下部分几何体的体积,即可得到它们之比.
(3)AB,BC,BB1两两互相垂直.以B为原点,建立如图所示的空间直角坐标系B-xyz,求出
,
,利cos<
,
>求直线AP与直线A1Q所成角的余弦值.
(2)说明AB为四棱锥A-BCQP的高,求出梯形BCQP的面积,即可求出平面APQ将三棱柱ABC-A1B1C1分成上部分的体积;同理求出下部分几何体的体积,即可得到它们之比.
(3)AB,BC,BB1两两互相垂直.以B为原点,建立如图所示的空间直角坐标系B-xyz,求出
| AP |
| A1Q |
| AP |
| A1Q |
解答: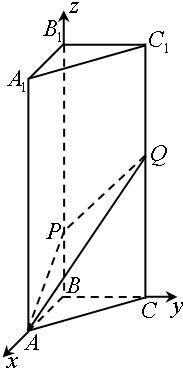 解:(1)证明:在正方形AA'A'1A1中,∵A'C=AA'-AB-BC=5,
解:(1)证明:在正方形AA'A'1A1中,∵A'C=AA'-AB-BC=5,
∴三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.∵AB=3,BC=4,
∴AB2+BC2=AC2,则AB⊥BC.∵四边形AA'A'1A1为正方形,AA1∥BB1,
∴AB⊥BB1,而BC∩BB1=B,∴AB⊥平面BCC1B1.
(2)解:∵AB⊥平面BCC1B1,∴AB为四棱锥A-BCQP的高.
∵四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
∴梯形BCQP的面积为SBCQP=
(BP+CQ)×BC=20,
∴四棱锥A-BCQP的体积VA-BCQP=
SBCPQ×AB=20,
由(1)知B1B⊥AB,B1B⊥BC,且AB∩BC=B,∴B1B⊥平面ABC.
∴三棱柱ABC-A1B1C1为直棱柱,
∴三棱柱ABC-A1B1C1的体积为VABC-A1B1C1=S△ABC•BB1=72.
故平面APQ将三棱柱ABC-A1B1C1分成上、下两部分的体积之比为
=
.
(3)解:由(1)、(2)可知,AB,BC,BB1两两互相垂直.
以B为原点,建立如图所示的空间直角坐标系B-xyz,
则A(3,0,0),A1(3,0,12),P(0,0,3),Q(0,4,7),
∴
=(-3,0,3),
=(-3,4,-5),∴cos<
,
>=
=-
,
∵异面直线所成角的范围为(0,
],
∴直线AP与A1Q所成角的余弦值为
.
 解:(1)证明:在正方形AA'A'1A1中,∵A'C=AA'-AB-BC=5,
解:(1)证明:在正方形AA'A'1A1中,∵A'C=AA'-AB-BC=5,∴三棱柱ABC-A1B1C1的底面三角形ABC的边AC=5.∵AB=3,BC=4,
∴AB2+BC2=AC2,则AB⊥BC.∵四边形AA'A'1A1为正方形,AA1∥BB1,
∴AB⊥BB1,而BC∩BB1=B,∴AB⊥平面BCC1B1.
(2)解:∵AB⊥平面BCC1B1,∴AB为四棱锥A-BCQP的高.
∵四边形BCQP为直角梯形,且BP=AB=3,CQ=AB+BC=7,
∴梯形BCQP的面积为SBCQP=
| 1 |
| 2 |
∴四棱锥A-BCQP的体积VA-BCQP=
| 1 |
| 3 |
由(1)知B1B⊥AB,B1B⊥BC,且AB∩BC=B,∴B1B⊥平面ABC.
∴三棱柱ABC-A1B1C1为直棱柱,
∴三棱柱ABC-A1B1C1的体积为VABC-A1B1C1=S△ABC•BB1=72.
故平面APQ将三棱柱ABC-A1B1C1分成上、下两部分的体积之比为
| 72-20 |
| 20 |
| 13 |
| 5 |
(3)解:由(1)、(2)可知,AB,BC,BB1两两互相垂直.
以B为原点,建立如图所示的空间直角坐标系B-xyz,
则A(3,0,0),A1(3,0,12),P(0,0,3),Q(0,4,7),
∴
| AP |
| A1Q |
| AP |
| A1Q |
| ||||
|
|
| 1 |
| 5 |
∵异面直线所成角的范围为(0,
| π |
| 2 |
∴直线AP与A1Q所成角的余弦值为
| 1 |
| 5 |
点评:本小题主要考查空间几何体中线面的位置关系,面积与体积,空间向量等基础知识,考查空间想象能力和运算求解能力.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
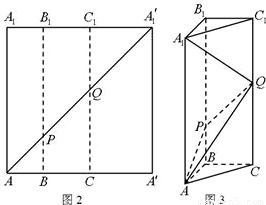 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.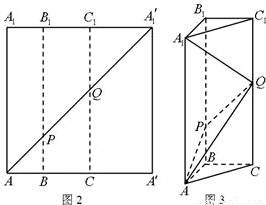 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.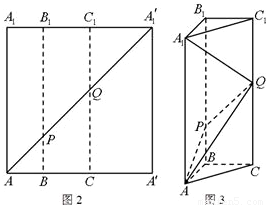 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.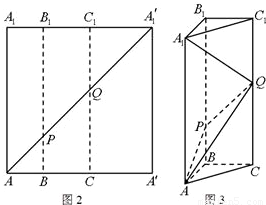 如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.
如图2所示,在边长为12的正方形AA'A'1A1中,点B,C在线段AA'上,且AB=3,BC=4,作BB1∥AA1,分别交A1A'1、AA'1于点B1、P,作CC1∥AA1,分别交A1A'1、AA'1于点C1、Q,将该正方形沿BB1、CC1折叠,使得A'A1′与AA1重合,构成如图3所示的三棱柱ABC-A1B1C1.