题目内容
已知球的表面积为20π,球面上有A、B、C三点,如果AB=AC=2,BC=2
,则球心到平面ABC的距离为( )
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |
分析:由已知中球的表面积为20π,我们可以求出球半径R,再由△ABC中,AB=AC=2,BC=2
,解三角形我们可以求出△ABC所在平面截球所得圆(即△ABC的外接圆半径),然后根据球心距d,球半径R,截面圆半径r,构造直角三角形,满足勾股定理,我们即可求出球心到平面ABC的距离.
| 3 |
解答:解:∵球的表面积为20π
∴球的半径R=
∵又AB=AC=2,BC=2
,
由余弦定理得CosA=-
则SinA=
则△ABC的外接圆半径2r=
=
=4
则r=2
则球心到平面ABC的距离d=
=1
故选A
∴球的半径R=
| 5 |
∵又AB=AC=2,BC=2
| 3 |
由余弦定理得CosA=-
| 1 |
| 2 |
则SinA=
| ||
| 2 |
则△ABC的外接圆半径2r=
| BC |
| SinA |
2
| ||||
|
则r=2
则球心到平面ABC的距离d=
| R2-r2 |
故选A
点评:本题考查的知识点是空间点、线、面之间的距离计算,其中根据球心距d,球半径R,截面圆半径r,构造直角三角形,满足勾股定理,是与球相关的距离问题常用方法.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
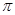 ,球面上有A、B、C三点,如果AB=AC=2,BC=2
,球面上有A、B、C三点,如果AB=AC=2,BC=2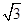 ,则球心到平面ABC的距离为( )
,则球心到平面ABC的距离为( )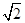 C.
C.