摘要：=+(n-1)d=+(n-k)d=+-d
网址：http://m.1010jiajiao.com/timu_id_490264[举报]
5、F（n）是一个关于自然数n的命题，若F（k）（k∈N+）真，则F（k+1）真，现已知F（7）不真，则有：①F（8）不真；②F（8）真；③F（6）不真；④F（6）真；⑤F（5）不真；⑥F（5）真．其中真命题是（ ）
查看习题详情和答案>>
（1）等差数列{an}中，an=3n-2，求首项 a1及公差d
（2）在等比数列{an}中，a3=2，a4=m，a5=8，求m的值；
（3）设公比为q（q≠1）的等比数列{an}的前n项和sn=qn+k，求k的值．
查看习题详情和答案>>
（2）在等比数列{an}中，a3=2，a4=m，a5=8，求m的值；
（3）设公比为q（q≠1）的等比数列{an}的前n项和sn=qn+k，求k的值．
（2012•惠州一模）甲乙两个学校高三年级分别有1200人，1000人，为了了解两个学校全体高三年级学生在该地区六校联考的数学成绩情况，采用分层抽样方法从两个学校一共抽取了110名学生的数学成绩，并作出了频数分布统计表如下：
甲校：
乙校：
（Ⅰ）计算x，y的值．
（Ⅱ）若规定考试成绩在[120，150]内为优秀，请分别估计两个学校数学成绩的优秀率．
（Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异．
参考数据与公式：
由列联表中数据计算K2=
临界值表
查看习题详情和答案>>
甲校：
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 3 | 4 | 8 | 15 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 15 | x | 3 | 2 |
| 分组 | [70，80） | [80，90） | [90，100） | [100，110） |
| 频数 | 1 | 2 | 8 | 9 |
| 分组 | [110，120） | [120，130） | [130，140） | [140，150] |
| 频数 | 10 | 10 | y | 3 |
| 甲校 | 乙校 | 总计 | |
| 优秀 | |||
| 非优秀 | |||
| 总计 |
（Ⅲ）由以上统计数据填写右面2×2列联表，并判断是否有90%的把握认为两个学校的数学成绩有差异．
参考数据与公式：
由列联表中数据计算K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
临界值表
| P（K≥k0） | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
（2006•宝山区二模）有一密码把英文的明文（真实文）按字母分解，其中a，b，…，z的26个字母（不论大小写）分别对应着1，2，…，26个自然数，见下表：
（x是奇数）（x是偶数）给出如下一个变换公式：x′=
，如8→
+13=17，即h变成q．按上述规定，若将明文译成密文是shxc，那么原来的明文是
查看习题详情和答案>>
| a | b | c | d | e | f | g | h | i | j | k | l | m |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| n | o | p | q | r | s | t | u | v | w | x | y | z |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 8 |
| 2 |
love
love
．
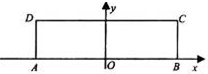（2013•日照一模）已知长方形ABCD，AB=2