题目内容
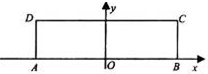 (2013•日照一模)已知长方形ABCD,AB=2
(2013•日照一模)已知长方形ABCD,AB=2| 2 |
| ||
| 3 |
(I)求以A,B为焦点,且过C,D两点的椭圆P的标准方程;
(Ⅱ)已知定点E(-1,0),直线y=kx+t与椭圆P交于M、N相异两点,证明:对作意的t>0,都存在实数k,使得以线段MN为直径的圆过E点.
分析:(I)设椭圆的标准方程是
+
=1(a>b>0),可得2a=AC+BC=即可得出a,又c=
,利用b2=a2-c2即可得出.
(II)把直线的方程与椭圆的方程联立即可得到根与系数的关系,再利用向量垂直与数量积的关系即可得出k与t的关系,再利用△>0即可证明.
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
(II)把直线的方程与椭圆的方程联立即可得到根与系数的关系,再利用向量垂直与数量积的关系即可得出k与t的关系,再利用△>0即可证明.
解答:解:(Ⅰ)由题意可得点A,B,C的坐标分别为(-
,0),(
,0),(
,
)
设椭圆的标准方程是
+
=1(a>b>0),
则2a=AC+BC=2
>2,∴a=
.
又c=
,
∴b2=a2-c2=1.
∴椭圆的标准方程是
+y2=1.
(Ⅱ)将y=kx+t代入椭圆方程,得(1+3k2)x2+6ktx+3t2-3=0,
由直线与椭圆有两个交点,所以△=(6kt)2-12(1+3k2)(t2-1)>0,解得k2>
.
设M(x1,y1)、N(x2,y2),则x1+x 2=-
,x1•x2=
,
∵以MN为直径的圆过E点,∴
•
=0,即(x1+1)(x2+1)+y1y2=0,
而y1y2=(kx1+t)(kx2+t)=k2x1x2+tk(x1+x2)+t2,
∴(k2+1)
-(tk+1)
+t2+1=0,解得k=
.
如果k2>
对任意的t>0都成立,则存在k,使得以线段MN为直径的圆过E点.
(
)2-
=
>0,即k2>
.
∴对任意的t>0,都存在k,使得以线段MN为直径的圆过E点.
| 2 |
| 2 |
| 2 |
| ||
| 3 |
设椭圆的标准方程是
| x2 |
| a2 |
| y2 |
| b2 |
则2a=AC+BC=2
| 3 |
| 3 |
又c=
| 2 |
∴b2=a2-c2=1.
∴椭圆的标准方程是
| x2 |
| 3 |
(Ⅱ)将y=kx+t代入椭圆方程,得(1+3k2)x2+6ktx+3t2-3=0,
由直线与椭圆有两个交点,所以△=(6kt)2-12(1+3k2)(t2-1)>0,解得k2>
| t2-1 |
| 3 |
设M(x1,y1)、N(x2,y2),则x1+x 2=-
| 6kt |
| 1+3k2 |
| 3(t2-1) |
| 1+3k2 |
∵以MN为直径的圆过E点,∴
| EM |
| EN |
而y1y2=(kx1+t)(kx2+t)=k2x1x2+tk(x1+x2)+t2,
∴(k2+1)
| 3(t2-1) |
| 1+3k2 |
| 6kt |
| 1+3k2 |
| 2t2-1 |
| 3t |
如果k2>
| t2-1 |
| 3 |
(
| 2t2-1 |
| 3t |
| t2-1 |
| 3 |
| (t2-1)2+t2 |
| 9t2 |
| t2-1 |
| 3 |
∴对任意的t>0,都存在k,使得以线段MN为直径的圆过E点.
点评:熟练掌握椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立、根与系数的关系、向量垂直与数量积的关系等是解题的关键.

练习册系列答案
相关题目