摘要: 判断函数单调性作差法:对带根号的一定要分子有理化.例如: 在进行讨论.
网址:http://m.1010jiajiao.com/timu_id_490204[举报]
(本小题满分12分)已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
,
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
【解析】第一问利用函数的奇函数性质可知f(0)=0
结合条件 ,解得函数解析式
,解得函数解析式
第二问中,利用函数单调性的定义,作差变形,定号,证明。
第三问中,结合第二问中的单调性,可知要是原式有意义的利用变量大,则函数值大的关系得到结论。
查看习题详情和答案>>
函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
(1)求实数a,b,并确定函数 的解析式;
的解析式;
(2)判断 在(-1,1)上的单调性,并用定义证明你的结论;
在(-1,1)上的单调性,并用定义证明你的结论;
(3)写出 的单调减区间,并判断
的单调减区间,并判断 有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
有无最大值或最小值?如有,写出最大值或最小值。(本小问不需要说明理由)
【解析】本试题主要考查了函数的解析式和奇偶性和单调性的综合运用。第一问中,利用函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 。
。
解得 ,
,
(2)中,利用单调性的定义,作差变形判定可得单调递增函数。
(3)中,由2知,单调减区间为 ,并由此得到当,x=-1时,
,并由此得到当,x=-1时, ,当x=1时,
,当x=1时,
解:(1) 是奇函数,
是奇函数, 。
。
即 ,
, ,
, ………………2分
………………2分
 ,又
,又 ,
, ,
, ,
,
(2)任取 ,且
,且 ,
,
 ,………………6分
,………………6分
 ,
,
 ,
, ,
, ,
, ,
,
 在(-1,1)上是增函数。…………………………………………8分
在(-1,1)上是增函数。…………………………………………8分
(3)单调减区间为 …………………………………………10分
…………………………………………10分
当,x=-1时, ,当x=1时,
,当x=1时, 。
。
查看习题详情和答案>>
已知函数f(x)=
+a是奇函数.
(1)求实数a的值;
(2)判断函数在R上的单调性并用函数单调性的定义证明;
(3)对任意的实数x,不等式f(x)>2m-1恒成立,求实数m的取值范围.
查看习题详情和答案>>
| 2x | 2x+1 |
(1)求实数a的值;
(2)判断函数在R上的单调性并用函数单调性的定义证明;
(3)对任意的实数x,不等式f(x)>2m-1恒成立,求实数m的取值范围.
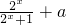 是奇函数.
是奇函数.