题目内容
(本小题满分12分)已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,
,
(1)确定函数 的解析式;
的解析式;
(2)用定义证明 在
在 上是增函数;
上是增函数;
(3)解不等式 .
.
【解析】第一问利用函数的奇函数性质可知f(0)=0
结合条件 ,解得函数解析式
,解得函数解析式
第二问中,利用函数单调性的定义,作差变形,定号,证明。
第三问中,结合第二问中的单调性,可知要是原式有意义的利用变量大,则函数值大的关系得到结论。
【答案】
(1)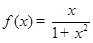 ;(2)见解析;(3)
;(2)见解析;(3)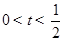 .
.
解:(1)依题意得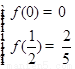 即
即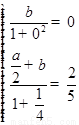 得
得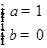
∴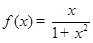
(2)证明:任取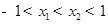 ,
,
则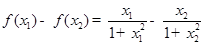
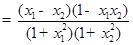
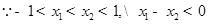 ,
,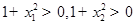
又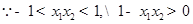
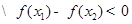
∴ 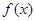 在
在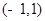 上是增函数。
上是增函数。
(3)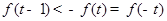
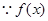 在
在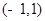 上是增函数,∴
上是增函数,∴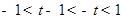 ,解得
,解得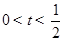 。
。

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目