题目内容
已知函数f(x)=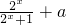 是奇函数.
是奇函数.
(1)求实数a的值;
(2)判断函数在R上的单调性并用函数单调性的定义证明;
(3)对任意的实数x,不等式f(x)>2m-1恒成立,求实数m的取值范围.
(1)由f(x)=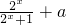 是奇函数,有f(-x)=-f(x),
是奇函数,有f(-x)=-f(x),
∴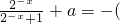
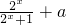 ),
),
∴2a=-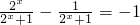 ,
,
∴a=- .
.
(2)f(x)在R上是增函数.
f(x)=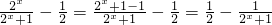
设x1、x2∈R且x1<x2,
f(x2)-f(x1)=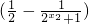 -
-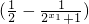
=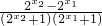 ,
,
∵x1<x2,∴ >
> ,
,
∴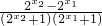 >0,即f(x2)>f(x1),
>0,即f(x2)>f(x1),
∴f(x)在R上是增函数.
(3)对任意的实数x,不等式f(x)>2m-1恒成立,
则只要2m-1<f(x)min,
∵2x+1>1∴0< <1,
<1,
∴-1<- <0,
<0,
- <
< -
- <
< ,即-
,即- <f(x)<
<f(x)< ,
,
∴2m-1≤- ,
,
∴m≤ .即m的取值范围为:(-∞,
.即m的取值范围为:(-∞, ].
].
分析:(1)由奇函数定义知,有f(-x)=-f(x)恒成立,由此可求a值;
(2)设x1、x2∈R且x1<x2,通过作差判断f(x2)与f(x1)的大小,利用函数单调性的定义可作出判断;
(3)对任意的实数x,不等式f(x)>2m-1恒成立,等价于2m-1<f(x)min,根据基本函数的值域可求出f(x)min.
点评:本题考查函数的奇偶性、单调性以及不等式恒成立问题,对于函数奇偶性、单调性常用定义解决,而恒成立则往往转化为函数最值问题.
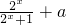 是奇函数,有f(-x)=-f(x),
是奇函数,有f(-x)=-f(x),∴
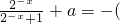
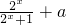 ),
),∴2a=-
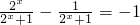 ,
,∴a=-
 .
.(2)f(x)在R上是增函数.
f(x)=
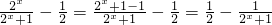
设x1、x2∈R且x1<x2,
f(x2)-f(x1)=
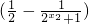 -
-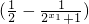
=
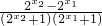 ,
,∵x1<x2,∴
 >
> ,
,∴
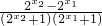 >0,即f(x2)>f(x1),
>0,即f(x2)>f(x1),∴f(x)在R上是增函数.
(3)对任意的实数x,不等式f(x)>2m-1恒成立,
则只要2m-1<f(x)min,
∵2x+1>1∴0<
 <1,
<1,∴-1<-
 <0,
<0,-
 <
< -
- <
< ,即-
,即- <f(x)<
<f(x)< ,
,∴2m-1≤-
 ,
,∴m≤
 .即m的取值范围为:(-∞,
.即m的取值范围为:(-∞, ].
].分析:(1)由奇函数定义知,有f(-x)=-f(x)恒成立,由此可求a值;
(2)设x1、x2∈R且x1<x2,通过作差判断f(x2)与f(x1)的大小,利用函数单调性的定义可作出判断;
(3)对任意的实数x,不等式f(x)>2m-1恒成立,等价于2m-1<f(x)min,根据基本函数的值域可求出f(x)min.
点评:本题考查函数的奇偶性、单调性以及不等式恒成立问题,对于函数奇偶性、单调性常用定义解决,而恒成立则往往转化为函数最值问题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
已知函数f(x+1)是偶函数,当x2>x1>1时,[f(x2)-f(x1)]( x2-x1)>0恒成立,设a=f (-
),b=f(2),c=f(3),则a,b,c的大小关系为( )
| 1 |
| 2 |
| A、b<a<c |
| B、c<b<a |
| C、b<c<a |
| D、a<b<c |