摘要：解:在矩阵N= 的作用下.一个图形变换为其绕原点逆时针旋转得到的图形.在矩阵M= 的作用下.一个图形变换为与之关于直线对称的图形.因此△ABC在矩阵MN作用下变换所得到的图形与△ABC全等.从而其面积等于△ABC的面积.即为1 八.坐标系与参数方程内 容要 求ABC
网址：http://m.1010jiajiao.com/timu_id_485124[举报]
（2012•三明模拟）（1）选修4-2：矩阵与变换
设矩阵M=
．
（I）若a=2，b=3，求矩阵M的逆矩阵M-1；
（II）若曲线C：x2+4xy+2y2=1在矩阵M的作用下变换成曲线C'：x2-2y2=1，求a+b的值．
（2）选修4-4：坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x轴的正半轴重合．圆C的参数方程为
（α为参数），点Q极坐标为(2，
)．
（Ⅰ）化圆C的参数方程为极坐标方程；
（Ⅱ）若点P是圆C上的任意一点，求P、Q两点距离的最小值．
（3）选修4-5：不等式选讲
设函数f（x）=|x+1|+|x-2|．
（Ⅰ）求y=f（x）的最小值；
（Ⅱ）若关于x的不等式f（x）≥4的解集为A，求集合A．
查看习题详情和答案>>
设矩阵M=
|
（I）若a=2，b=3，求矩阵M的逆矩阵M-1；
（II）若曲线C：x2+4xy+2y2=1在矩阵M的作用下变换成曲线C'：x2-2y2=1，求a+b的值．
（2）选修4-4：坐标系与参数方程
已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中x轴的正半轴重合．圆C的参数方程为
|
| 7π |
| 4 |
（Ⅰ）化圆C的参数方程为极坐标方程；
（Ⅱ）若点P是圆C上的任意一点，求P、Q两点距离的最小值．
（3）选修4-5：不等式选讲
设函数f（x）=|x+1|+|x-2|．
（Ⅰ）求y=f（x）的最小值；
（Ⅱ）若关于x的不等式f（x）≥4的解集为A，求集合A．
形如
的式子叫做二行二列矩阵，定义矩阵的一种运算
•
=
．该运算的几何意义为平面上的点（x，y）在矩阵
的作用下变换成点（ax+by，cx+dy）．
（1）设点M（-2，1）在
的作用下变换成点M′，求点M′的坐标；
（2）设数列{an} 的前n项和为Sn ，且对任意正整数n，点A（Sn，n）在
的作用下变换成的点A′在函数f（x）=x2+x的图象上，求an的表达式；
（3）在（2）的条件下，设bn为数列{1-
}的前n项的积，是否存在实数a使得不等式bn
＜a对一切n∈N*都成立？若存在，求a的取值范围；若不存在，请说明理由．
查看习题详情和答案>>
|
|
|
|
|
（1）设点M（-2，1）在
|
（2）设数列{an} 的前n项和为Sn ，且对任意正整数n，点A（Sn，n）在
|
（3）在（2）的条件下，设bn为数列{1-
| 1 |
| an |
| an+1 |
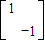，N=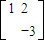
，求直线y=2x+1在矩阵MN的作用下变换所得到的直线方程．