题目内容
形如
|
|
|
|
|
(1)设点M(-2,1)在
|
(2)设数列{an} 的前n项和为Sn ,且对任意正整数n,点A(Sn,n)在
|
(3)在(2)的条件下,设bn为数列{1-
| 1 |
| an |
| an+1 |
分析:(1)根据二阶矩阵与平面列向量的乘法的乘法规则,将问题转化为矩阵的计算;
(2)由题意Sn=n2+n,从而可求an的表达式;
(3)构造函数,利用函数的单调性解决恒成立问题.
(2)由题意Sn=n2+n,从而可求an的表达式;
(3)构造函数,利用函数的单调性解决恒成立问题.
解答:解:(1)∵
=
∴点M′的坐标为(1,-2);
(2)∵
=
,∴A′(n,Sn)
∵点A′(n,Sn)在函数f(x)=x2+x的图象上,∴Sn=n2+n
当n=1时,a1=S1=2
当n≥2时,an=Sn-Sn-1=2n
a1=2满足上式,∴an=2nn∈N*
(3)bn=(1-
)(1-
)(1-
),设Fn=(1-
)(1-
)(1-
)
∵
=
<1
∴F(n)>F(n+1),F(n)单调递减.
∴当n=1时,F(n)取最大值
要使不等式bn
<a对一切n∈N*都成立,只需a>
所以a的取值范围为(
,+∞)
|
|
|
(2)∵
|
|
|
∵点A′(n,Sn)在函数f(x)=x2+x的图象上,∴Sn=n2+n
当n=1时,a1=S1=2
当n≥2时,an=Sn-Sn-1=2n
a1=2满足上式,∴an=2nn∈N*
(3)bn=(1-
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| an |
| 2n+1 |
∵
| F(n+1) |
| F(N) |
| ||||
| 2n+2 |
∴F(n)>F(n+1),F(n)单调递减.
∴当n=1时,F(n)取最大值
| ||
| 2 |
要使不等式bn
| an+1 |
| ||
| 2 |
所以a的取值范围为(
| ||
| 2 |
点评:在二阶矩阵对应的变换作用下,它将平面上任意一个点(向量)(x,y)对应惟一的一个平面点(向量)(x′,y′).数列中的恒成立问题,通常可借助于构造的函数的单调性进行解决.

练习册系列答案
相关题目
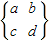 的式子叫做二行二列矩阵,定义矩阵的一种运算
的式子叫做二行二列矩阵,定义矩阵的一种运算
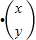 =
=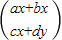 .该运算的几何意义为平面上的点(x,y)在矩阵
.该运算的几何意义为平面上的点(x,y)在矩阵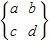 的作用下变换成点(ax+by,cx+dy).
的作用下变换成点(ax+by,cx+dy).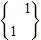 的作用下变换成点M′,求点M′的坐标;
的作用下变换成点M′,求点M′的坐标;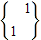 的作用下变换成的点A′在函数f(x)=x2+x的图象上,求an的表达式;
的作用下变换成的点A′在函数f(x)=x2+x的图象上,求an的表达式;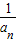 }的前n项的积,是否存在实数a使得不等式
}的前n项的积,是否存在实数a使得不等式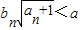 对一切n∈N*都成立?若存在,求a的取值范围;若不存在,请说明理由.
对一切n∈N*都成立?若存在,求a的取值范围;若不存在,请说明理由.