题目内容
已知矩阵M=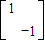 ,N=
,N=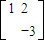 ,求直线y=2x+1在矩阵MN的作用下变换所得到的直线方程.
,求直线y=2x+1在矩阵MN的作用下变换所得到的直线方程.
【答案】分析:MN=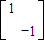
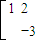 =
= ,设y=2x+1上一点(x,y)在MN作用下变为(x′,y′),则
,设y=2x+1上一点(x,y)在MN作用下变为(x′,y′),则
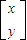 =
= ,由此得到
,由此得到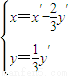 ,再由y=2x+1,得到6x′-5y′+3=0,所以变换后的直线方程是6x-5y+3=0.
,再由y=2x+1,得到6x′-5y′+3=0,所以变换后的直线方程是6x-5y+3=0.
解答:解:∵MN=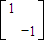
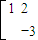 =
= ,
,
设y=2x+1上一点(x,y)在MN作用下变为(x′,y′),
则
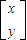 =
= ,
,
∴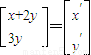 ,
,
∴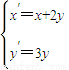 ,∴
,∴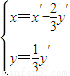 ,
,
∵y=2x+1,代入得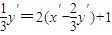 ,
,
化简,得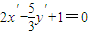 ,
,
即6x′-5y′+3=0,
∴变换后的直线方程是:6x-5y+3=0.
点评:本题考查二阶矩阵的变换,解题时要认真审题,注意公式的灵活运用.
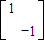
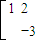 =
= ,设y=2x+1上一点(x,y)在MN作用下变为(x′,y′),则
,设y=2x+1上一点(x,y)在MN作用下变为(x′,y′),则
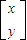 =
= ,由此得到
,由此得到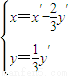 ,再由y=2x+1,得到6x′-5y′+3=0,所以变换后的直线方程是6x-5y+3=0.
,再由y=2x+1,得到6x′-5y′+3=0,所以变换后的直线方程是6x-5y+3=0.解答:解:∵MN=
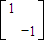
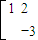 =
= ,
,设y=2x+1上一点(x,y)在MN作用下变为(x′,y′),
则

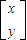 =
= ,
,∴
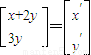 ,
,∴
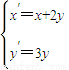 ,∴
,∴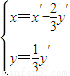 ,
,∵y=2x+1,代入得
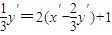 ,
,化简,得
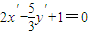 ,
,即6x′-5y′+3=0,
∴变换后的直线方程是:6x-5y+3=0.
点评:本题考查二阶矩阵的变换,解题时要认真审题,注意公式的灵活运用.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 ,N=
,N= ,且MN=
,且MN= 。
。 =2
=2 sin
sin 。
。 3的解集为
3的解集为 ,求实数a的值;
,求实数a的值;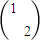 ,N=
,N=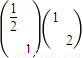 ,矩阵MN对应的变换把曲线
,矩阵MN对应的变换把曲线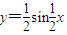 变为曲线C,求曲线C的方程.
变为曲线C,求曲线C的方程.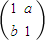 ,N=
,N=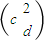 ,且MN=
,且MN=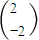 .
.