摘要:因为.平面.所以平面.
网址:http://m.1010jiajiao.com/timu_id_484922[举报]
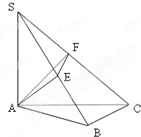 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:要证AF⊥SC
只需证 SC⊥平面AEF
只需证 AE⊥SC(因为EF⊥SC)
只需证 AE⊥平面SBC
只需证
①
①
(因为AE⊥SB)只需证 BC⊥平面SAB
只需证
②
②
(因为AB⊥BC)由只需证 SA⊥平面ABC可知上式成立
所以AF⊥SC
把证明过程补充完整①
AE⊥BC
AE⊥BC
②BC⊥SA
BC⊥SA
.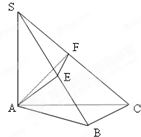 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
要证AF⊥SC
只需证 SC⊥平面AEF
只需证 AE⊥SC(因为EF⊥SC)
只需证 AE⊥平面SBC
只需证________(因为AE⊥SB)
只需证 BC⊥平面SAB
只需证________(因为AB⊥BC)
由只需证 SA⊥平面ABC可知上式成立
所以AF⊥SC
把证明过程补充完整①________②________.
查看习题详情和答案>>
请先阅读:
设平面向量
=(a1,a2),
=(b1,b2),且
与
的夹角为θ,
因为
•
=|
||
|cosθ,
所以
•
≤|
||
|.
即a1b1+a2b2≤
×
,
当且仅当θ=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有(a1b1+a2b2+a3b3)2≤(
+
+
)(
+
+
)成立;
(II)试求函数y=
+
+
的最大值.
查看习题详情和答案>>
设平面向量
| a |
| b |
| a |
| b |
因为
| a |
| b |
| a |
| b |
所以
| a |
| b |
| a |
| b |
即a1b1+a2b2≤
|
|
当且仅当θ=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有(a1b1+a2b2+a3b3)2≤(
| a | 2 1 |
| a | 2 2 |
| a | 2 3 |
| b | 2 1 |
| b | 2 2 |
| b | 2 3 |
(II)试求函数y=
| x |
| 2x-2 |
| 8-3x |