题目内容
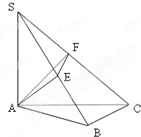 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:要证AF⊥SC
只需证 SC⊥平面AEF
只需证 AE⊥SC(因为EF⊥SC)
只需证 AE⊥平面SBC
只需证
①
①
(因为AE⊥SB)只需证 BC⊥平面SAB
只需证
②
②
(因为AB⊥BC)由只需证 SA⊥平面ABC可知上式成立
所以AF⊥SC
把证明过程补充完整①
AE⊥BC
AE⊥BC
②BC⊥SA
BC⊥SA
.分析:根据线面垂直的判定,只需证明直线垂直于平面内的两条相交直线,由此可得结论.
解答:解:根据线面垂直的判定,要证明AE⊥平面SBC,因为AE⊥SB,所以只需证AE⊥BC,即①为AE⊥BC;
要证BC⊥平面SAB,因为AB⊥BC,所以只需证BC⊥SA,即②为BC⊥SA
故答案为AE⊥BC;BC⊥SA.
要证BC⊥平面SAB,因为AB⊥BC,所以只需证BC⊥SA,即②为BC⊥SA
故答案为AE⊥BC;BC⊥SA.
点评:本题考查线面垂直,考查学生分析解决问题的能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 如图,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC、SC于点D、E,又SA=AB,SB=BC,求二面角E-BD-C的大小.
如图,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分SC,且分别交AC、SC于点D、E,又SA=AB,SB=BC,求二面角E-BD-C的大小.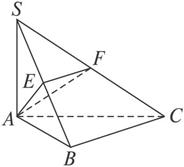
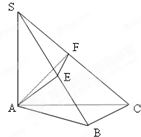 如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程:
如图SA⊥平面ABC,AB⊥BC,过A做SB的垂线,垂足为E,过E做SC的垂线,垂足为F,求证AF⊥SC.以下是证明过程: