题目内容
请先阅读:
设平面向量![]() =(a1,a2),
=(a1,a2),![]() =(b1,b2),且
=(b1,b2),且![]() 与
与![]() 的夹角为è,
的夹角为è,
因为![]() •
•![]() =|
=|![]() ||
||![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() ||
||![]() |.
|.
即![]() ,
,
当且仅当è=0时,等号成立.
(I)利用上述想法(或其他方法),结合空间向量,证明:对于任意a1,a2,a3,b1,b2,b3∈R,都有![]() 成立;
成立;
(II)试求函数![]() 的最大值.
的最大值.
考点:
平面向量的综合题.
专题:
平面向量及应用.
分析:
(I)利用![]() •
•![]() ≤|
≤|![]() |•|
|•|![]() |,即可证明结论;
|,即可证明结论;
(II)构造空间向量![]() =(1,1,1),
=(1,1,1),![]() ,且
,且![]() 与
与![]() 的夹角为è,利用(I)的结论,即可得到结论.
的夹角为è,利用(I)的结论,即可得到结论.
解答:
(I)证明:设空间向量![]() =(a1,a2,a3),
=(a1,a2,a3),![]() =(b1,b2,b3),且
=(b1,b2,b3),且![]() 与
与![]() 的夹角为è,
的夹角为è,
因为![]() •
•![]() =|
=|![]() |•|
|•|![]() |cosè,
|cosè,
所以![]() •
•![]() ≤|
≤|![]() |•|
|•|![]() |,(3分)
|,(3分)
即![]() (6分)
(6分)
所以![]() ,
,
当且仅当è=0时,等号成立.(7分)
(II)解:设空间向量![]() =(1,1,1),
=(1,1,1),![]() ,且
,且![]() 与
与![]() 的夹角为è,(9分)
的夹角为è,(9分)
因为![]() ,
,
所以![]() ,
,
即![]() ,(12分)
,(12分)
当且仅当è=0(即![]() 与
与![]() 共线,且方向相同)时,等号成立.
共线,且方向相同)时,等号成立.
所以当![]() 时,
时,
即x=2时,函数![]() 有最大值
有最大值![]() .(14分)
.(14分)
点评:
本题考查向量的数量积公式,考查函数最大值的求解,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
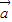 =(a1,a2),
=(a1,a2),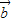 =(b1,b2),且
=(b1,b2),且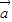 与
与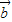 的夹角为θ,
的夹角为θ,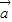 •
•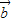 =|
=|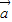 ||
||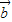 |cosθ,
|cosθ,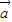 •
•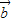 ≤|
≤|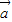 ||
||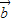 |.
|.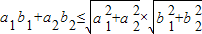 ,
,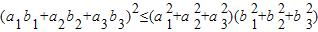 成立;
成立;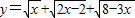 的最大值.
的最大值.