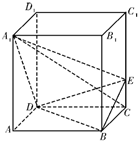（2012•湖南模拟）如图，正四棱柱ABCD-A₁B₁C₁D₁（即底面为正方形的直四棱柱）中，AA₁=2AB=4，点 E 在 CC₁ 上且 C₁E=3EC．
（1）证明：A₁C丄平面BED；
（2）求直线A₁C与平面A₁DE所成角的正弦值．

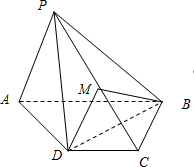（2012•河南模拟）如图，在四棱锥P-ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD=2AD=8，AB=2DC=4

5

．
（I）设M是PC上的一点，证明：平面MBD⊥平面PAD；
（Ⅱ）求三棱锥C-PAB的体积．

（2012•河南模拟）如图，在四棱锥P-ABCD中，∠ABC=∠ACD=90°，∠BAC=∠CAD=60°，PA⊥平面ABCD，E为PD的中点，AB=1，PA=2．
（Ⅰ）证明：直线CE∥平面PAB；
（Ⅱ）求三棱锥E-PAC的体积．

（2009•成都模拟）如图，在四棱锥P-ABCD中，底面ABCD为正方形，且PD⊥平面ABCD，PD=AB=1，EF分别是PB、AD的中点，
（I）证明：EF∥平面PCD；
（Ⅱ）求二面角B-CE-F的大小．

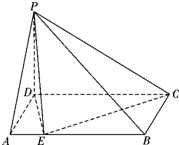（2012•武汉模拟）如图，在四棱锥P-ABCD中，底面ABCD为矩形，PD⊥底面ABCD，E是AB上一点．已知PD=

2

，CD=4，AD=

3

．
（Ⅰ）若∠ADE=

π

6

，求证：CE⊥平面PDE；
（Ⅱ）当点A到平面PDE的距离为

2 21

7

时，求三棱锥A-PDE的侧面积．