Question

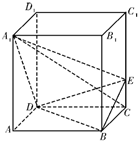（2012•湖南模拟）如图，正四棱柱ABCD-A₁B₁C₁D₁（即底面为正方形的直四棱柱）中，AA₁=2AB=4，点 E 在 CC₁ 上且 C₁E=3EC．
（1）证明：A₁C丄平面BED；
（2）求直线A₁C与平面A₁DE所成角的正弦值．

Answer 1

分析：（1）以DA为x轴，以DC为y轴，以DD₁为z轴，建立空间直角坐标系，则

A1C

=(-2，2，-4)，

DB

=(2，2，0)，

DE

=(0，2，1)，由向量法能够证明A₁C丄平面BED．
（2）由

A1E

=(-2，2，-3)，

A1D

=(-2，0，-4)，求出平面A₁DE的法向量

n

=(-4，-1，2)，取

A1C

=（-2，2，-4），
设直线A₁C与平面A₁DE所成角为θ，由sinθ=|cos＜

n

，

A1C

＞|能求出直线A₁C与平面A₁DE所成角的正弦值．

解答：（1）证明：如图，以DA为x轴，以DC为y轴，以DD₁为z轴，建立空间直角坐标系，
则A₁（2，0，4），B（2，2，0），C（0，2，0），D（0，0，0），E（0，2，1）
∴

A1C

=(-2，2，-4)，

DB

=(2，2，0)，

DE

=(0，2，1)，
∵

A1C

•

DB

=-2×2+2×2-4×0=0，

A1C

•

DE

=-2× 0+2×2-4×1=0，
∴

A1C

⊥

DB

，

A1C

⊥

DE

，
∴A₁C丄平面BED．
（2）解：∵

A1E

=(-2，2，-3)，

A1D

=(-2，0，-4)，
设平面A₁DE的法向量为

n

=(x，y，z)，
∵

n

•

A1E

=0，

n

•

A1D

=0，
∴

-2x+2y-3z=0 -2x-4z=0

，
取

n

=(-4，-1，2)，

A1C

=（-2，2，-4），
设直线A₁C与平面A₁DE所成角为θ，
则sinθ=|cos＜

n

，

A1C

＞|=|

8-2-8

21 • 24

|=

14

42

，
∴直线A₁C与平面A₁DE所成角的正弦值为

14

42

．

点评：本题考查直线与平面垂直的证明和求直线与平面所成角的正弦值的求法，解题时要认真审题，合理地建立空间直角坐标系，注意向量法的灵活运用．