题目内容
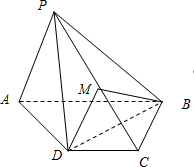 (2012•河南模拟)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4
(2012•河南模拟)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥DC,△PAD是等边三角形,已知BD=2AD=8,AB=2DC=4| 5 |
(I)设M是PC上的一点,证明:平面MBD⊥平面PAD;
(Ⅱ)求三棱锥C-PAB的体积.
分析:(Ⅰ)在△ABD中,由题意可得AD2+BD2=AB2,故AD⊥BD;由平面PAD⊥平面ABCD的性质定理可得,BD⊥平面PAD,最后由面面垂直的判定定理即可证得平面MBD⊥平面PAD;
(Ⅱ)过P作PO⊥AD交AD于O,则PO⊥平面ABCD,△PAD是边长为4的等边三角形,可求得PO=2
,由V棱锥C-PAB=V棱锥P-ABC即可求得答案.
(Ⅱ)过P作PO⊥AD交AD于O,则PO⊥平面ABCD,△PAD是边长为4的等边三角形,可求得PO=2
| 3 |
解答:证明:(Ⅰ)∵在△ABD中,由于AD=4AB=4
,BD=8,
∴AD2+BD2=AB2,
∴AD⊥BD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD?平面ABCD,
∴BD⊥平面PAD.…(4分)
又BD?平面MBD,
∴平面MBD⊥平面PAD.
(Ⅱ)过P作PO⊥AD交AD于O,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD.
∴PO为棱锥P-ABC的高.
又△PAD是边长为4的等边三角形,
∴PO=
×4=2
.
又S△ABC=S△ABD
=
•AD•BD
=16,
∴V棱锥C-PAB=V棱锥P-ABC
=
×16×2
=
.
| 5 |
∴AD2+BD2=AB2,
∴AD⊥BD,
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD?平面ABCD,
∴BD⊥平面PAD.…(4分)
又BD?平面MBD,
∴平面MBD⊥平面PAD.
(Ⅱ)过P作PO⊥AD交AD于O,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,
∴PO⊥平面ABCD.
∴PO为棱锥P-ABC的高.
又△PAD是边长为4的等边三角形,
∴PO=
| ||
| 2 |
| 3 |
又S△ABC=S△ABD
=
| 1 |
| 2 |
=16,
∴V棱锥C-PAB=V棱锥P-ABC
=
| 1 |
| 3 |
| 3 |
=
32
| ||
| 3 |
点评:本题考查平面与平面垂直的判定,考查棱锥的体积,熟练掌握线面垂直、面面垂直的判定定理是解决问题的先决条件,注重锥体体积轮换公式的考查,属于中档题.

练习册系列答案
相关题目
 (2012•河南模拟)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,AD=2AB=2PA,E为PD的上一点,且PE=2ED,F为PC的中点.
(2012•河南模拟)如图,在四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为矩形,AD=2AB=2PA,E为PD的上一点,且PE=2ED,F为PC的中点.