摘要：(与重合舍去)．
网址：http://m.1010jiajiao.com/timu_id_474874[举报]
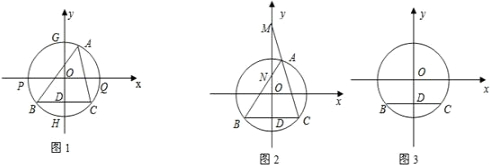
如图，在平面直角坐标系中，以O为圆心，以
的长为半径作⊙O交x轴于P、Q两点，交y轴于G、H两点，△ABC内接于⊙O，且BC∥x轴交y轴于D，∠BAC=45°（如图1）．
（1）求C点坐标；
（2）若点A在x轴上方的半圆上运动（不与G重合），且CA的延长线交y轴于M，AB交y轴于N（如图2），当A点运动时，ON•OM的值是否发生变化？若变化，说明理由；若不变，求出其值；
（3）若点A在⊙O上运动（不与B、C重合），是否存在点A，使△ABC为等腰三角形？若存在，请求出A点坐标；若不存在，请说明理由．
查看习题详情和答案>>
| 2 |
（1）求C点坐标；
（2）若点A在x轴上方的半圆上运动（不与G重合），且CA的延长线交y轴于M，AB交y轴于N（如图2），当A点运动时，ON•OM的值是否发生变化？若变化，说明理由；若不变，求出其值；
（3）若点A在⊙O上运动（不与B、C重合），是否存在点A，使△ABC为等腰三角形？若存在，请求出A点坐标；若不存在，请说明理由．
查看习题详情和答案>>
如图1，在△ABC中，∠ACB=90°，∠CAB=30°，△ABD是等边三角形，E是AB的中点，连接CE并延长交AD于F．
（1）求证：①△AEF≌△BEC；②四边形BCFD是平行四边形；
（2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，求sin∠ACH的值．
查看习题详情和答案>>
（1）求证：①△AEF≌△BEC；②四边形BCFD是平行四边形；
（2）如图2，将四边形ACBD折叠，使D与C重合，HK为折痕，求sin∠ACH的值．
查看习题详情和答案>>
如图，把矩形OABC放置在直角坐标系中，OA=6，OC=8，若将矩形折叠，使点B与O重合，得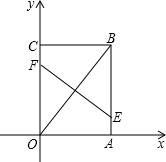
到折痕EF．
（1）可以通过 办法，使四边形AEFO变到四边形BEFC的位置（填“平移”、“旋转”或“翻转”）；
（2）写出点E在坐标系中的位置即点E的坐标 ；
（3）折痕EF的长为 ；
（4）若直线l把矩形OABC的面积分成相等的两部分，则直线l必经过点 ，写出经过这点的任意一条直线的函数关系式 ．
查看习题详情和答案>>
到折痕EF．（1）可以通过
（2）写出点E在坐标系中的位置即点E的坐标
（3）折痕EF的长为
（4）若直线l把矩形OABC的面积分成相等的两部分，则直线l必经过点
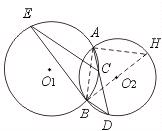16、已知：如图，⊙O1与⊙O2相交于A、B两点，经过A点的直线分别交⊙O1、⊙O2于C、D两点（C、D不与B重合），连接BD，过点C作BD的平行线交⊙O1于点E，连BE．
如图，射线AM∥BN，∠A=∠B=90°，点D、C分别在AM、BN上运动（点D不与A重合、点C不与B重合），E是AB边上的动点（点E不与A、B重合），在运动过程中始终保持DE⊥EC且AD+DE=AB=a．