题目内容
如图,把矩形OABC放置在直角坐标系中,OA=6,OC=8,若将矩形折叠,使点B与O重合,得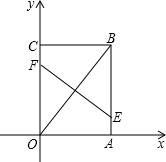 到折痕EF.
到折痕EF.(1)可以通过
(2)写出点E在坐标系中的位置即点E的坐标
(3)折痕EF的长为
(4)若直线l把矩形OABC的面积分成相等的两部分,则直线l必经过点
分析:由折叠后的已知条件可以证得△ONF∽△OAB代入已知条件从而解得.
解答: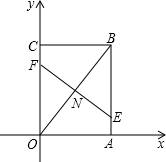 解:设EF与OB相交于点N,
解:设EF与OB相交于点N,
由题意折叠
∴EF⊥OB,ON=NB,
又∵矩形OABC,
∴AB∥OC,
∴∠OFE=∠BEF,又∠FNO=∠ENB,ON=BN,
∴△OFN≌△EBN,
∴FN=EN,OF=BE,
∵四边形OABC是矩形
∴∠FOB=∠OBA
∴△OFN∽△OAB
∴
=
又∵知道AB=8,OA=6
∴FN=3.75
∴EF=7.5
∴OF=BE=6.25
∴AE=8-6.25=1.75
∵点E在第一象限内
∴点E(6,1.75);
由题意知直线L必经过矩形的对角线交点
则由题意其交点坐标横坐标为矩形宽的一半即为3,纵坐标为矩形长的一半为4.
即由题意一条直线经过原点即设为y=kx
代入(3,4)得y=
x.
 解:设EF与OB相交于点N,
解:设EF与OB相交于点N,由题意折叠
∴EF⊥OB,ON=NB,
又∵矩形OABC,
∴AB∥OC,
∴∠OFE=∠BEF,又∠FNO=∠ENB,ON=BN,
∴△OFN≌△EBN,
∴FN=EN,OF=BE,
∵四边形OABC是矩形
∴∠FOB=∠OBA
∴△OFN∽△OAB
∴
| ON |
| AB |
| NF |
| OA |
又∵知道AB=8,OA=6
∴FN=3.75
∴EF=7.5
∴OF=BE=6.25
∴AE=8-6.25=1.75
∵点E在第一象限内
∴点E(6,1.75);
由题意知直线L必经过矩形的对角线交点
则由题意其交点坐标横坐标为矩形宽的一半即为3,纵坐标为矩形长的一半为4.
即由题意一条直线经过原点即设为y=kx
代入(3,4)得y=
| 4 |
| 3 |
点评:本题考查了一次函数的应用,通过折叠后所得到的已知条件从而解得.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
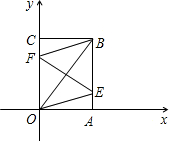 到折痕EF,连接OE、BF.
到折痕EF,连接OE、BF. 21、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形OA′B′C′,则点B′的坐标为( )
21、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形OA′B′C′,则点B′的坐标为( ) 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为( )
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为( )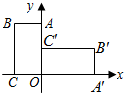 17、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=1,OA=2,把矩形OABC绕着原点顺时针旋转90°得到矩形OA'B'C',则点B'的坐标为
17、如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=1,OA=2,把矩形OABC绕着原点顺时针旋转90°得到矩形OA'B'C',则点B'的坐标为