摘要:直线的方程为.与联立得
网址:http://m.1010jiajiao.com/timu_id_471429[举报]
在平面直角坐标系 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值.
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)曲线 与
与 轴的交点为(0,1),
轴的交点为(0,1),
与 轴的交点为(3+2
轴的交点为(3+2 ,0),(3-2
,0),(3-2 ,0) 故可设
,0) 故可设 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因为圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 。联立方程组得到结论。
。联立方程组得到结论。
查看习题详情和答案>>
如图,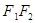 分别是椭圆
分别是椭圆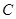 :
: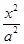 +
+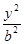 =1(
=1(
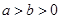 )的左、右焦点,
)的左、右焦点,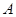 是椭圆
是椭圆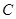 的顶点,
的顶点,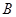 是直线
是直线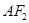 与椭圆
与椭圆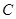 的另一个交点,
的另一个交点,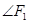
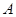
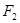 =60°.
=60°.
(Ⅰ)求椭圆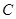 的离心率;
的离心率;
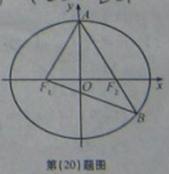
(Ⅱ)已知△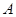
 的面积为40
的面积为40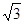 ,求
,求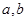 的值.
的值.
【解析】 (Ⅰ)由题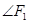
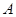
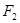 =60°,则
=60°,则 ,即椭圆
,即椭圆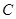 的离心率为
的离心率为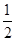 。
。
(Ⅱ)因△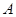
 的面积为40
的面积为40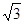 ,设
,设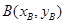 ,又面积公式
,又面积公式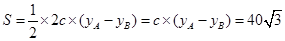 ,又直线
,又直线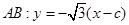 ,
,
又由(Ⅰ)知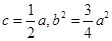 ,联立方程可得
,联立方程可得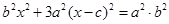 ,整理得
,整理得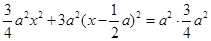 ,解得
,解得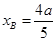 ,
,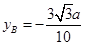 ,所以
,所以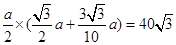 ,解得
,解得 。
。
查看习题详情和答案>>
设椭圆E:  (a,b>0)过M(2,
(a,b>0)过M(2,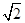 ) ,N(
) ,N(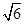 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且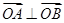 ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。
【解析】本试题主要是考查了椭圆方程的求解,待定系数法求解,并且考查了圆与椭圆的位置关系的研究,利用恒有交点,联立方程组和韦达定理一起表示向量OA,OB,并证明垂直。
查看习题详情和答案>>
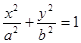 (a,b>0)过M(2,
(a,b>0)过M(2,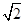 ) ,N(
) ,N(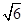 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点, ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。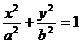 (a,b>0)过M(2,
(a,b>0)过M(2,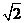 )
,N(
)
,N(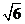 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,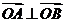 ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。