题目内容
在平面直角坐标系 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值.
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)曲线 与
与 轴的交点为(0,1),
轴的交点为(0,1),
与 轴的交点为(3+2
轴的交点为(3+2 ,0),(3-2
,0),(3-2 ,0) 故可设
,0) 故可设 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因为圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 。联立方程组得到结论。
。联立方程组得到结论。
【答案】
(1) (x-3)2+(y-1)2=9
(2) 
解: (1)曲线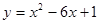 与
与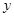 轴的交点为(0,1),
轴的交点为(0,1),
与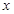 轴的交点为(3+2
轴的交点为(3+2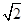 ,0),(3-2
,0),(3-2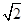 ,0).………………2分
,0).………………2分
故可设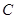 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2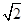 )2+t2,解得t=1.
)2+t2,解得t=1.
则圆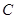 的半径为
的半径为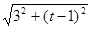 =3.所以圆
=3.所以圆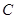 的方程为(x-3)2+(y-1)2=9. ………6分
的方程为(x-3)2+(y-1)2=9. ………6分
(2)设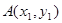 ,
,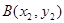 ,其坐标满足方程组
,其坐标满足方程组
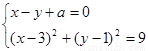
消去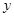 ,得到方程
,得到方程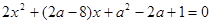 ………………8分
………………8分
由已知可得,判别式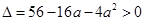 .从而
.从而
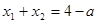 ,
,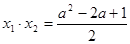 .① ……………10分
.① ……………10分
由于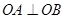 ,可得
,可得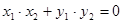
又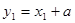 ,
,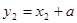 ,所以
,所以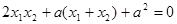 ②…………………12分
②…………………12分
由①,②得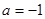 ,满足
,满足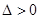 ,故
,故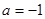 .…………………14分
.…………………14分

练习册系列答案
相关题目