题目内容
设椭圆E: 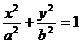 (a,b>0)过M(2,
(a,b>0)过M(2,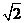 )
,N(
)
,N(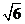 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,
(1)求椭圆E的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且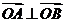 ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。
【解析】本试题主要是考查了椭圆方程的求解,待定系数法求解,并且考查了圆与椭圆的位置关系的研究,利用恒有交点,联立方程组和韦达定理一起表示向量OA,OB,并证明垂直。
【答案】
解:(1)因为椭圆E: 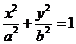 (a,b>0)过M(2,
(a,b>0)过M(2,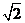 ) ,N(
) ,N(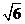 ,1)两点,
,1)两点,
所以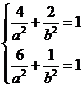 解得
解得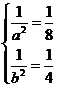 所以
所以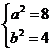 椭圆E的方程为
椭圆E的方程为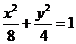
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且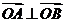 ,设该圆的切线方程为
,设该圆的切线方程为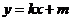 解方程组
解方程组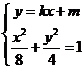 得
得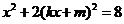 ,即
,即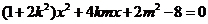 ,
,
则△=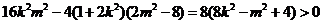 ,即
,即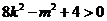
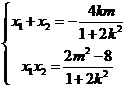 ,
, 要使
要使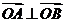 ,需使
,需使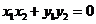 ,即
,即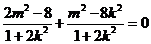 ,所以
,所以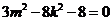 ,所以
,所以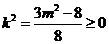 又
又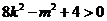 ,所以
,所以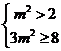 ,所以
,所以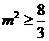 ,即
,即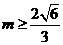 或
或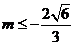 ,因为直线
,因为直线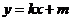 为圆心在原点的圆的一条切线,所以圆的半径为
为圆心在原点的圆的一条切线,所以圆的半径为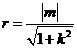 ,
,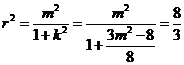 ,
,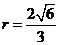 ,所求的圆为
,所求的圆为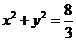 ,此时圆的切线
,此时圆的切线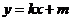 都满足
都满足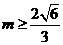 或
或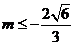 ,而当切线的斜率不存在时切线为
,而当切线的斜率不存在时切线为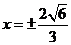 与椭圆
与椭圆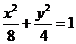 的两个交点为
的两个交点为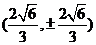 或
或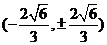 满足
满足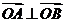 ,综上, 存在圆心在原点的圆
,综上, 存在圆心在原点的圆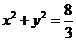 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且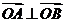

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
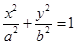 (a,b>0)过M(2,
(a,b>0)过M(2,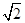 ) ,N(
) ,N(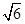 ,1)两点,O为坐标原点.
,1)两点,O为坐标原点.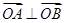 ?若存在,写出该圆的方程,若不存在说明理由。
?若存在,写出该圆的方程,若不存在说明理由。 (a,b>0)过M(2,
(a,b>0)过M(2, )
,N(
)
,N(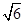 ,1)两点,O为坐标原点,
,1)两点,O为坐标原点,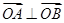 ?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在说明理由
?若存在,写出该圆的方程,并求|AB|的取值范围,若不存在说明理由 (a,b>0)过M(2,
(a,b>0)过M(2, ) ,N(
) ,N( ,1)两点,O为坐标原点,(I)求椭圆E的方程;
,1)两点,O为坐标原点,(I)求椭圆E的方程; ?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。
?若存在,写出该圆的方程,并求|AB |的取值范围,若不存在说明理由。