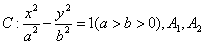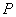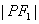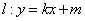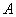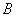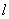摘要:(Ⅰ)当为定值时.求证为定值(与无关).并求出这个定值,
网址:http://m.1010jiajiao.com/timu_id_469764[举报]
给定椭圆![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为![]() ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为![]() .
.
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的一个动点,过点P作直线![]() ,使得
,使得![]() 与椭圆C都只有一个交点,且
与椭圆C都只有一个交点,且![]() 分别交其“准圆”于点M,N .
分别交其“准圆”于点M,N .
(1)当P为“准圆”与![]() 轴正半轴的交点时,求
轴正半轴的交点时,求![]() 的方程;
的方程;
(2)求证:|MN|为定值.
查看习题详情和答案>> 。
。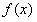 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围; 只有一个零点;
只有一个零点;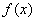 的图象与x轴交于
的图象与x轴交于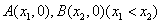 两点,AB中点为
两点,AB中点为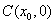 ,求证:
,求证: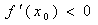 。
。 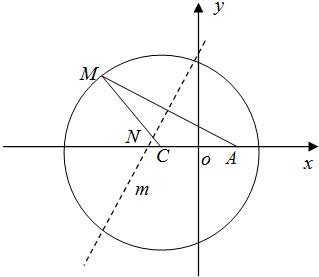 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.