题目内容
己知 。
。
(Ⅰ)若a=-1,函数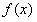 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;
(Ⅱ)当a=1,b=-1时,证明函数 只有一个零点;
只有一个零点;
(Ⅲ)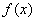 的图象与x轴交于
的图象与x轴交于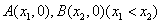 两点,AB中点为
两点,AB中点为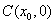 ,求证:
,求证: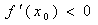 。
。
 。
。(Ⅰ)若a=-1,函数
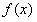 在其定义域内是增函数,求b的取值范围;
在其定义域内是增函数,求b的取值范围;(Ⅱ)当a=1,b=-1时,证明函数
 只有一个零点;
只有一个零点;(Ⅲ)
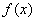 的图象与x轴交于
的图象与x轴交于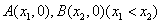 两点,AB中点为
两点,AB中点为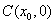 ,求证:
,求证: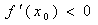 。
。 解:(Ⅰ)依题意, ,
,
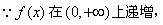
∴
即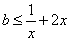 对
对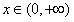 恒成立,
恒成立,
∴只需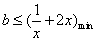 ,
,
∵x>0,
∴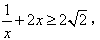
当且仅当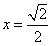 时,等号成立,
时,等号成立,
∴
∴
(Ⅱ)当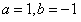 时,
时,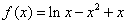 ,
,
其定义域为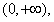
∴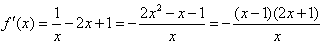 ,
,
∵x>0,
∴当0<x<1时, 0;
0;
当x>1时,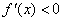 ;
;
∴
∴ ,
,
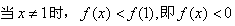 ,
,
∴函数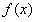 只有一个零点。
只有一个零点。
(Ⅲ)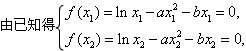
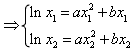 ,
,
两式相减得
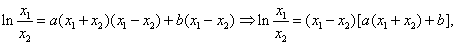
由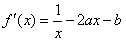 及
及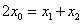 ,得
,得

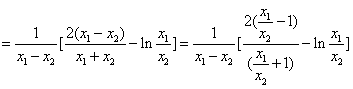 ,
,
令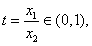 且
且 ,
,
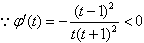 ,
,
∴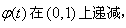
∴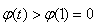 ,
,
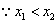 ,
,
∴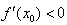 。
。
 ,
,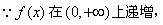
∴

即
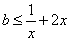 对
对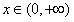 恒成立,
恒成立,∴只需
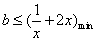 ,
,∵x>0,
∴
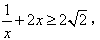
当且仅当
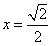 时,等号成立,
时,等号成立,∴

∴

(Ⅱ)当
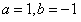 时,
时,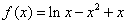 ,
,其定义域为
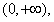
∴
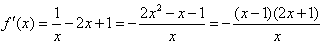 ,
,∵x>0,
∴当0<x<1时,
 0;
0;当x>1时,
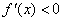 ;
;∴

∴
 ,
,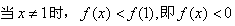 ,
,∴函数
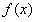 只有一个零点。
只有一个零点。(Ⅲ)
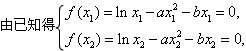
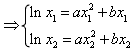 ,
,两式相减得
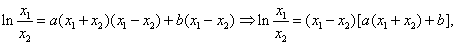
由
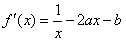 及
及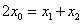 ,得
,得
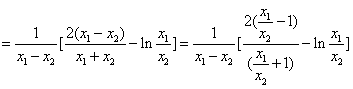 ,
,令
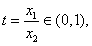 且
且 ,
,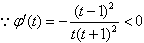 ,
,∴
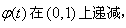
∴
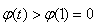 ,
,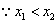 ,
,∴
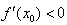 。
。
练习册系列答案
相关题目
 (a>b>0)的两个焦点,若椭圆上存在一点P使得
(a>b>0)的两个焦点,若椭圆上存在一点P使得 ,则椭圆的离心率e的取值范围为________.
,则椭圆的离心率e的取值范围为________.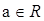 为虚数单位,若(1-2i)(a +i)为纯虚数,则a的值等于( )
为虚数单位,若(1-2i)(a +i)为纯虚数,则a的值等于( )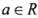 为虚数单位,若(1-2i)(a +i)为纯虚数,则a的值等于( )
为虚数单位,若(1-2i)(a +i)为纯虚数,则a的值等于( )