题目内容
 (1)设
(1)设 为椭圆
为椭圆 的左焦点,证明:当且仅当椭圆
的左焦点,证明:当且仅当椭圆 上的点
上的点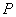 在椭圆的左、右顶点时,
在椭圆的左、右顶点时,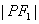 取得最小值与最大值;
取得最小值与最大值;
(2)若椭圆 上的点到焦点距离的最大值为3,最小值为l,求椭圆
上的点到焦点距离的最大值为3,最小值为l,求椭圆 的标准方程;
的标准方程;
(3)若直线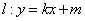 与(2)中所述椭圆
与(2)中所述椭圆 相交于
相交于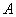 、
、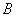 两点(
两点(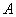 、
、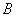 不是左右顶点),且满是
不是左右顶点),且满是 ,求证:直线
,求证:直线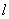 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
 (1)设
(1)设 为椭圆
为椭圆 的左焦点,证明:当且仅当椭圆
的左焦点,证明:当且仅当椭圆 上的点
上的点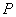 在椭圆的左、右顶点时,
在椭圆的左、右顶点时,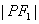 取得最小值与最大值;
取得最小值与最大值;
(2)若椭圆 上的点到焦点距离的最大值为3,最小值为l,求椭圆
上的点到焦点距离的最大值为3,最小值为l,求椭圆 的标准方程;
的标准方程;
(3)若直线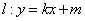 与(2)中所述椭圆
与(2)中所述椭圆 相交于
相交于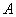 、
、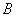 两点(
两点(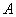 、
、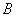 不是左右顶点),且满是
不是左右顶点),且满是 ,求证:直线
,求证:直线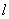 过定点,并求出该定点坐标.
过定点,并求出该定点坐标.
 名校课堂系列答案
名校课堂系列答案