题目内容
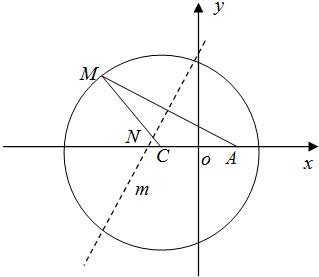 如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.
如图,点A为圆形纸片内不同于圆心C的定点,动点M在圆周上,将纸片折起,使点M与点A重合,设折痕m交线段CM于点N.现将圆形纸片放在平面直角坐标系xoy中,设圆C:(x+1)2+y2=4a2(a>1),A(1,0),记点N的轨迹为曲线E.(1)证明曲线E是椭圆,并写出当a=2时该椭圆的标准方程;
(2)设直线l过点C和椭圆E的上顶点B,点A关于直线l的对称点为点Q,若椭圆E的离心率e∈[
| 1 |
| 2 |
| ||
| 2 |
分析:(1)依题意知NA=NM,N的轨迹是以C、A为焦点,长轴长为2a,焦距为2的椭圆.由题高级条件能求出其椭圆方程.
(2)设椭圆的标准方程为
+
=1,直线l的方程为
+
=1,设Q(x,y),由点Q与点A(1,0)关于直线l对称,知
,消去x,得y=
.再由e∈[
,
]可推导出点Q的纵坐标的取值范围.
(2)设椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
| x |
| -1 |
| y |
| b |
|
| 4b |
| b2+1 |
| 1 |
| 2 |
| ||
| 2 |
解答:解:(1)依题意:直线m为线段AM的垂直平分线,∴NA=NM,
∴NC+NA=NC+NM=2a>2,
∴N的轨迹是以C、A为焦点,长轴长为2a,焦距为2的椭圆.
当a=2时,长轴长为2a=4,焦距为2c=2,∴b2=3.
∴椭圆方程为
+
=1.
(2)设椭圆的标准方程为
+
=1,由(1)知:b2=a2-1,
又C(-1,0),B(0,b),
∴直线l的方程为
+
=1,即bx-y+b=0.
设Q(x,y),∵点Q与点A(1,0)关于直线l对称,
∴
,消去x,得y=
.
∵e∈[
,
],∴
≤
≤
,
∴
≤a2≤4,∴
≤b2+1≤4,∴
≤b≤
.
∴y=
=
≤
=2,当且仅当b=1时取等号,
又当b=
时,y=
,当b=
时,y=
,
∴点Q的纵坐标的取值范围是[
,2].
∴NC+NA=NC+NM=2a>2,
∴N的轨迹是以C、A为焦点,长轴长为2a,焦距为2的椭圆.
当a=2时,长轴长为2a=4,焦距为2c=2,∴b2=3.
∴椭圆方程为
| x2 |
| 4 |
| y2 |
| 3 |
(2)设椭圆的标准方程为
| x2 |
| 4 |
| y2 |
| 3 |
又C(-1,0),B(0,b),
∴直线l的方程为
| x |
| -1 |
| y |
| b |
设Q(x,y),∵点Q与点A(1,0)关于直线l对称,
∴
|
| 4b |
| b2+1 |
∵e∈[
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| a2 |
| 3 |
| 4 |
∴
| 4 |
| 3 |
| 4 |
| 3 |
| ||
| 3 |
| 3 |
∴y=
| 4b |
| b2+1 |
| 4 | ||
b+
|
| 4 |
| 2 |
又当b=
| 3 |
| 3 |
| ||
| 3 |
| 3 |
∴点Q的纵坐标的取值范围是[
| 3 |
点评:本题考查圆锥曲线的性质和应用,难度较大,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( )
3、如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( ) 如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,MF的垂直平分线CD交OM于P,则点P的轨迹是( )
如图,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,MF的垂直平分线CD交OM于P,则点P的轨迹是( )
 )
) )
)