题目内容
给定椭圆![]() ,称圆心在原点
,称圆心在原点![]() ,半径为
,半径为![]() 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为![]() ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为![]() .
.
(Ⅰ)求椭圆C的方程和其“准圆”方程;
(Ⅱ)点P是椭圆C的“准圆”上的一个动点,过点P作直线![]() ,使得
,使得![]() 与椭圆C都只有一个交点,且
与椭圆C都只有一个交点,且![]() 分别交其“准圆”于点M,N .
分别交其“准圆”于点M,N .
(1)当P为“准圆”与![]() 轴正半轴的交点时,求
轴正半轴的交点时,求![]() 的方程;
的方程;
(2)求证:|MN|为定值.
(I)因为![]() ,所以
,所以![]()
所以椭圆的方程为![]() ,
,
又![]() =2, 所以准圆的方程为
=2, 所以准圆的方程为![]() .
.
(II)(1)因为准圆![]() 与
与![]() 轴正半轴的交点为P(0,2),
轴正半轴的交点为P(0,2),
设过点P(0,2),且与椭圆有一个公共点的直线为![]() ,
,
所以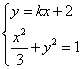 ,消去y ,得到
,消去y ,得到![]() ,
,
因为椭圆与![]() 只有一个公共点, 所以
只有一个公共点, 所以![]() ,
,
解得![]() .所以
.所以![]() 方程为
方程为![]() .
.
(2)①当![]() 中有一条无斜率时,不妨设
中有一条无斜率时,不妨设![]() 无斜率,
无斜率,
因为![]() 与椭圆只有一个公共点,则其方程为
与椭圆只有一个公共点,则其方程为![]() 或
或![]() ,
,
当![]() 方程为
方程为![]() 时,此时
时,此时![]() 与准圆交于点
与准圆交于点![]() ,
,
此时经过点![]() (或
(或![]() )且与椭圆只有一个公共点的直线是
)且与椭圆只有一个公共点的直线是
![]() (或
(或![]() ),即
),即![]() 为
为![]() (或
(或![]() ),显然直线
),显然直线![]() 垂直;
垂直;
同理可证 ![]() 方程为
方程为![]() 时,直线
时,直线![]() 垂直.
垂直.
② 当![]() 都有斜率时,设点
都有斜率时,设点![]() ,其中
,其中![]() ,
,
设经过点![]() 与椭圆只有一个公共点的直线为
与椭圆只有一个公共点的直线为![]() ,
,
则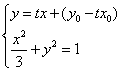 ,消去
,消去![]() 得到
得到![]() ,
,
即![]() ,
,
![]() ,
,
经过化简得到:![]() ,
,
因为![]() ,所以有
,所以有![]() ,
,
设![]() 的斜率分别为
的斜率分别为![]() ,因为
,因为![]() 与椭圆都只有一个公共点,
与椭圆都只有一个公共点,
所以![]() 满足上述方程
满足上述方程![]() ,
,
所以![]() ,即
,即![]() 垂直.
垂直.
综合①②知:
因为![]() 经过点
经过点![]() ,又分别交其准圆于点M,N,且
,又分别交其准圆于点M,N,且![]() 垂直,
垂直,
所以线段MN为准圆![]() 的直径,所以|MN|=4.
的直径,所以|MN|=4.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
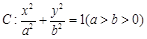 ,称圆心在原点
,称圆心在原点 ,半径为
,半径为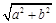 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为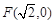 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为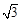 .
. ,使得
,使得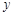 轴正半轴的交点时,求
轴正半轴的交点时,求 ,称圆心在原点O,半径为
,称圆心在原点O,半径为 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为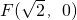 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为 .
.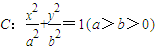 ,称圆心在原点O,半径为
,称圆心在原点O,半径为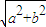 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为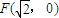 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为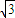 .
.