网址:http://m.1010jiajiao.com/timu_id_467699[举报]
在平面直角坐标系 中,曲线
中,曲线 与坐标轴的交点都在圆
与坐标轴的交点都在圆 上.
上.
(1)求圆 的方程;
的方程;
(2)若圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 ,求
,求 的值.
的值.
【解析】本试题主要是考查了直线与圆的位置关系的运用。
(1)曲线 与
与 轴的交点为(0,1),
轴的交点为(0,1),
与 轴的交点为(3+2
轴的交点为(3+2 ,0),(3-2
,0),(3-2 ,0) 故可设
,0) 故可设 的圆心为(3,t),则有32+(t-1)2=(2
的圆心为(3,t),则有32+(t-1)2=(2 )2+t2,解得t=1.
)2+t2,解得t=1.
(2)因为圆 与直线
与直线 交于
交于 、
、 两点,且
两点,且 。联立方程组得到结论。
。联立方程组得到结论。
查看习题详情和答案>>
已知椭圆
 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当 <
< 时,求实数
时,求实数 的取值范围.
的取值范围.
【解析】本试题主要考查了椭圆的方程以及直线与椭圆的位置关系的运用。
第一问中,利用
第二问中,利用直线与椭圆联系,可知得到一元二次方程中 ,可得k的范围,然后利用向量的
,可得k的范围,然后利用向量的 <
< 不等式,表示得到t的范围。
不等式,表示得到t的范围。
解:(1)由题意知

查看习题详情和答案>>
已知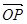 =
=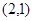 ,
,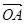 =
=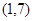 ,
, =
=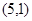 ,设
,设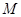 是直线
是直线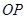 上一点,
上一点,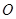 是坐标原点.
是坐标原点.
⑴求使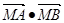 取最小值时的
取最小值时的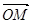 ;
⑵对(1)中的点
;
⑵对(1)中的点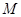 ,求
,求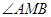 的余弦值.
的余弦值.
【解析】第一问中利用设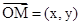 ,则根据已知条件,O,M,P三点共线,则可以得到x=2y,然后利用
,则根据已知条件,O,M,P三点共线,则可以得到x=2y,然后利用
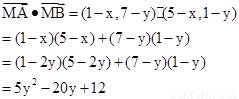
可知当x=4,y=2时取得最小值。
第二问中利用数量积的性质可以表示夹角的余弦值,进而得到结论。
(1)、因为设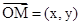 则
则
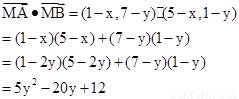
可知当x=4,y=2时取得最小值。此时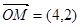 。
。
(2)
查看习题详情和答案>>
已知椭圆的长轴长为 ,焦点是
,焦点是 ,点
,点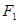 到直线
到直线 的距离为
的距离为 ,过点
,过点 且倾斜角为锐角的直线
且倾斜角为锐角的直线 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得 .
.
(1)求椭圆的标准方程; (2)求直线l的方程.
【解析】(1)中利用点F1到直线x=- 的距离为
的距离为 可知-
可知- +
+ =
= .得到a2=4而c=
.得到a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
得到椭圆的方程。(2)中,利用 ,设出点A(x1,y1)、B(x2,y2).,借助于向量公式
,设出点A(x1,y1)、B(x2,y2).,借助于向量公式 再利用 A、B在椭圆
再利用 A、B在椭圆 +y2=1上, 得到坐标的值,然后求解得到直线方程。
+y2=1上, 得到坐标的值,然后求解得到直线方程。
解:(1)∵F1到直线x=- 的距离为
的距离为 ,∴-
,∴- +
+ =
= .
.
∴a2=4而c= ,∴b2=a2-c2=1.
,∴b2=a2-c2=1.
∵椭圆的焦点在x轴上,∴所求椭圆的方程为 +y2=1.……4分
+y2=1.……4分
(2)设A(x1,y1)、B(x2,y2).由第(1)问知
 ,
,
∴ ……6分
……6分
∵A、B在椭圆 +y2=1上,
+y2=1上,
∴ ……10分
……10分
∴l的斜率为 =
= .
.
∴l的方程为y= (x-
(x- ),即
),即 x-y-
x-y- =0.
=0.
查看习题详情和答案>>
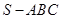 中,平面
中,平面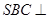 平面
平面 ,
,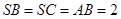 ,
,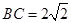 ,
,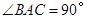 ,
,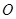 为
为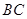 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角 的余弦值.
的余弦值.
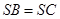 ,
,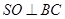
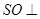 平面
平面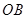 、
、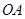 、
、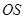 为
为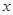 ,
,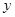 ,
,
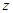 轴建立直角坐标系得
轴建立直角坐标系得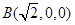 ,
,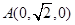 ,
,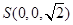 ,
,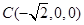 ,
,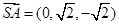 ,
,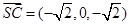 ,
, 而
而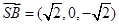 ,故点B到平面
,故点B到平面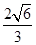
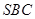 的法向量
的法向量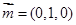 ,平面
,平面