题目内容
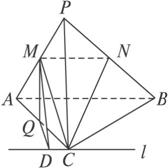
如图,在三棱锥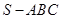 中,平面
中,平面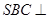 平面
平面 ,
,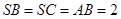 ,
,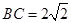 ,
,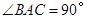 ,
,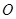 为
为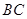 中点.(Ⅰ)求点B到平面
中点.(Ⅰ)求点B到平面 的距离;(Ⅱ)求二面角
的距离;(Ⅱ)求二面角 的余弦值.
的余弦值.

【解析】第一问中利用因为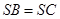 ,
,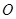 为
为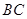 中点,所以
中点,所以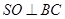
而平面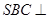 平面
平面 ,所以
,所以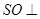 平面
平面 ,再由题设条件知道可以分别以
,再由题设条件知道可以分别以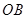 、
、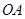 、
、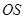 为
为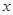 ,
,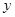 ,
,
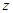 轴建立直角坐标系得
轴建立直角坐标系得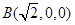 ,
,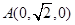 ,
,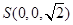 ,
,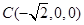 ,
,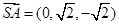 ,
,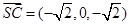 ,
,
故平面 的法向量
的法向量 而
而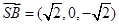 ,故点B到平面
,故点B到平面 的距离
的距离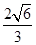
第二问中,由已知得平面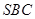 的法向量
的法向量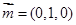 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于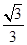
解:(Ⅰ)因为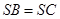 ,
,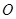 为
为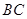 中点,所以
中点,所以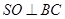
而平面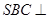 平面
平面 ,所以
,所以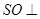 平面
平面 ,
,
再由题设条件知道可以分别以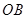 、
、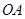 、
、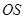 为
为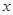 ,
,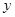 ,
,
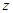 轴建立直角坐标系,得
轴建立直角坐标系,得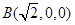 ,
,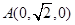 ,
,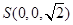 ,
,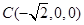 ,
,
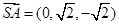 ,
,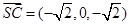 ,故平面
,故平面 的法向量
的法向量
而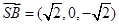 ,故点B到平面
,故点B到平面 的距离
的距离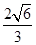
(Ⅱ)由已知得平面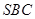 的法向量
的法向量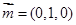 ,平面
,平面 的法向量
的法向量
故二面角 的余弦值等于
的余弦值等于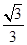
【答案】
(Ⅰ)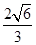 (Ⅱ)
(Ⅱ)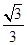

练习册系列答案
相关题目
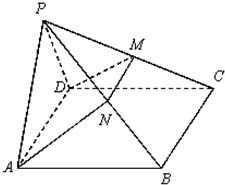 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD是边长为2的菱形,∠BAD=60°,N是PB中点,过A、N、D三点的平面交PC于M. (2013•青岛一模)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A、N、D三点的平面交PC于M.
(2013•青岛一模)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,N是PB中点,过A、N、D三点的平面交PC于M.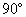 ,∠B=
,∠B=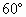 ,PC⊥平面ABC,AB=8,PC=6,M,N分别是PA,PB的中点,设△MNC所在平面与△ABC所在平面交于直线l.(1)判断l与MN的位置关系;(2)求点M到l的距离.
,PC⊥平面ABC,AB=8,PC=6,M,N分别是PA,PB的中点,设△MNC所在平面与△ABC所在平面交于直线l.(1)判断l与MN的位置关系;(2)求点M到l的距离.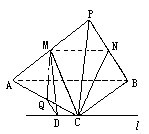
 如图,在四棱锥
如图,在四棱锥