摘要:令由此可知
网址:http://m.1010jiajiao.com/timu_id_457953[举报]
已知M、N两点的坐标分别是![]() 是常数
是常数![]() ,令
,令![]() 是坐标原点
是坐标原点![]() .
.
(Ⅰ)求函数![]() 的解析式,并求函数
的解析式,并求函数![]() 在
在![]() 上的单调递增区间;
上的单调递增区间;
(Ⅱ)当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,求a的值,并说明此时
,求a的值,并说明此时![]() 的图象可由函数
的图象可由函数![]() 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?
已知曲线 的方程为
的方程为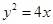 ,过原点作斜率为
,过原点作斜率为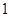 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为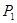 ,过
,过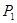 作斜率为
作斜率为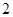 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为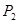 ,过
,过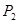 作斜率为
作斜率为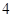 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为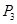 ,如此下去,一般地,过点
,如此下去,一般地,过点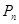 作斜率为
作斜率为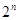 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为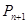 ,设点
,设点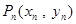 (
( ).
).
(1)指出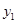 ,并求
,并求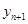 与
与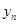 的关系式(
的关系式( );
);
(2)求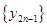 (
( )的通项公式,并指出点列
)的通项公式,并指出点列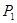 ,
,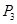 , ,
, ,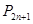 , 向哪一点无限接近?说明理由;
, 向哪一点无限接近?说明理由;
(3)令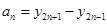 ,数列
,数列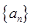 的前
的前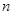 项和为
项和为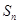 ,设
,设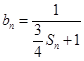 ,求所有可能的乘积
,求所有可能的乘积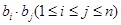 的和.
的和.
已知M、N两点的坐标分别是M(1+cos2x,1)、N(1, sin2x+a)(x,a∈R,a是常数),令f(x)=
sin2x+a)(x,a∈R,a是常数),令f(x)= ·
· (O是坐标原点).
(O是坐标原点).
(1)求函数f(x)的解析式,并求函数f(x)在[0,π]上的单调递增区间;
(2)当x∈[0,![]() ]时,f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由函数y=2sin(x+
]时,f(x)的最大值为4,求a的值,并说明此时f(x)的图象可由函数y=2sin(x+![]() )的图象经过怎样的平移和伸缩变换而得到.
)的图象经过怎样的平移和伸缩变换而得到.
 是常数
是常数 ,令
,令 是坐标原点
是坐标原点 的解析式,并求函数
的解析式,并求函数 上的单调递增区间;
上的单调递增区间; 时,
时, ,求a的值,并说明此时
,求a的值,并说明此时 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?