题目内容
已知曲线 的方程为
的方程为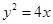 ,过原点作斜率为
,过原点作斜率为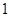 的直线和曲线
的直线和曲线 相交,另一个交点记为
相交,另一个交点记为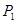 ,过
,过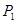 作斜率为
作斜率为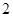 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为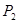 ,过
,过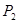 作斜率为
作斜率为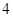 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为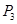 ,如此下去,一般地,过点
,如此下去,一般地,过点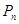 作斜率为
作斜率为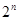 的直线与曲线
的直线与曲线 相交,另一个交点记为
相交,另一个交点记为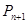 ,设点
,设点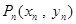 (
(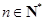 ).
).
(1)指出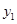 ,并求
,并求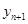 与
与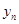 的关系式(
的关系式(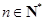 );
);
(2)求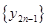 (
(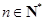 )的通项公式,并指出点列
)的通项公式,并指出点列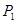 ,
,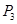 , ,
, ,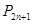 , 向哪一点无限接近?说明理由;
, 向哪一点无限接近?说明理由;
(3)令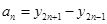 ,数列
,数列 的前
的前 项和为
项和为 ,设
,设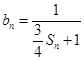 ,求所有可能的乘积
,求所有可能的乘积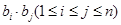 的和.
的和.
(1)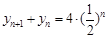 ;(2)
;(2)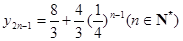 ,
,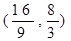 ;(3)
;(3)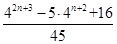 .
.
解析试题分析:(1)由于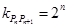 ,点
,点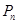 ,
,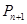 又都是抛物线上的点,代入进去变形可得到
又都是抛物线上的点,代入进去变形可得到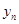 与
与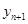 的关系为
的关系为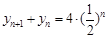 ;(2)由于只要求数列
;(2)由于只要求数列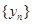 的奇数项,因此把(1)中得到的关系式中
的奇数项,因此把(1)中得到的关系式中 分别为
分别为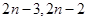 代换,得到两个等式相减可得
代换,得到两个等式相减可得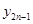 与
与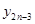 的关系式
的关系式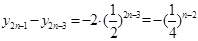 ,用累加法可求得通项公式
,用累加法可求得通项公式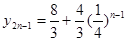 ,当
,当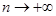 时,
时,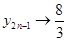 ,即得极限点为
,即得极限点为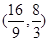 ;(3)求出
;(3)求出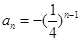 ,是一个等比数列,其
,是一个等比数列,其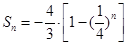 ,于是
,于是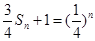 ,即
,即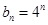 ,要求和
,要求和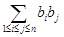 ,可先求和
,可先求和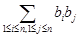 ,而
,而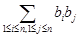
 ,
,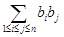
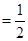
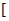
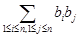
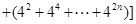 ,由此可得结论.
,由此可得结论.
试题解析:(1)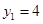 . (1分)
. (1分)
设 ,
,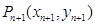 ,由题意得
,由题意得 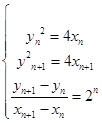 . (2分)
. (2分)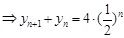 (4分)
(4分)
(2)分别用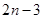 、
、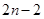 代换上式中的n得
代换上式中的n得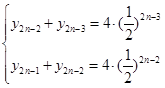
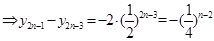 (
(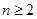 ) (6分)
) (6分)
又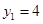 ,
,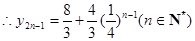 , (8分)
, (8分)
因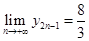 ,所以点列
,所以点列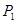 ,
,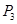 , ,
, ,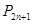 , 向点
, 向点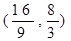 无限接近. (10分)
无限接近. (10分)
(3)(理)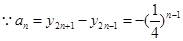 ,
,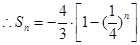 . (11分)
. (11分)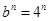 ,
,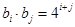
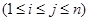 . (12分)
. (12分)
将所得的积排成如下矩阵: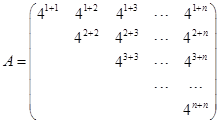 ,设矩阵
,设矩阵 的各项和为
的各项和为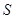 .
.
在矩阵的左下方补上相应的数可得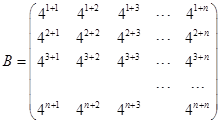
矩阵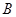 中第一行的各数和
中第一行的各数和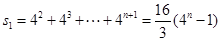 ,
,
矩阵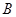 中第二行的各数和
中第二行的各数和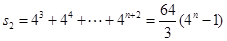 ,
,
矩阵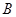 中第
中第 行的各数和
行的各数和 ,
,

练习册系列答案
相关题目
 过点
过点 ,且离心率
,且离心率 .
. 的直线
的直线 与该椭圆相交于A、B两点,试问:在直线
与该椭圆相交于A、B两点,试问:在直线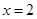 上是否存在点P,使得
上是否存在点P,使得 是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.
是正三角形?若存在,求出点P的坐标;若不存在,请说明理由.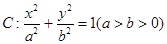 .称圆心在原点O,半径为
.称圆心在原点O,半径为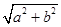 的圆是椭圆C的“准圆”.若椭圆C的一个焦点为
的圆是椭圆C的“准圆”.若椭圆C的一个焦点为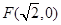 ,其短轴上的一个端点到F的距离为
,其短轴上的一个端点到F的距离为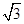 .
. ,使得
,使得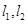 与椭圆C都只有一个交点,试判断
与椭圆C都只有一个交点,试判断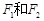 ,且点
,且点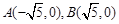 在椭圆C上,又
在椭圆C上,又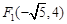 .
.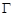 的方程;
的方程;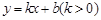 与曲线
与曲线 中,已知定点F(1,0),点
中,已知定点F(1,0),点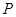 在
在 轴上运动,点
轴上运动,点 在
在 轴上,点
轴上,点
 ,
, .
.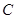 的方程;
的方程; 是直线
是直线 :
: 上任意一点,过点
上任意一点,过点 ,
, ,切点分别为
,切点分别为 ,
, ,设切线
,设切线 ,
, ,直线
,直线 的斜率为
的斜率为 ,求证:
,求证: .
. :
: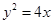 和
和 :
:
 的焦点分别为
的焦点分别为 ,
, 交于
交于 两点(
两点( 为坐标原点),且
为坐标原点),且
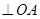 .
. ,交
,交 ,点
,点 坐标为
坐标为 ,求△
,求△ 面积的最小值.
面积的最小值. = 2
= 2 ,求直线l的方程.
,求直线l的方程.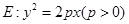 的准线与x轴交于点M,过点M作圆
的准线与x轴交于点M,过点M作圆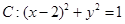 的两条切线,切点为A、B,
的两条切线,切点为A、B,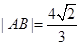 .
. 的离心率为
的离心率为 ,过左焦点
,过左焦点 且斜率为
且斜率为 的直线交椭圆E于A,B两点,线段AB的中点为M,直线
的直线交椭圆E于A,B两点,线段AB的中点为M,直线 :
: 交椭圆E于C,D两点.
交椭圆E于C,D两点.