题目内容
已知M、N两点的坐标分别是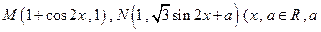 是常数
是常数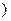 ,令
,令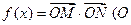 是坐标原点
是坐标原点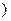 .
.
(Ⅰ)求函数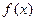 的解析式,并求函数
的解析式,并求函数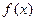 在
在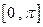 上的单调递增区间;
上的单调递增区间;
(Ⅱ)当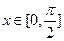 时,
时,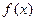 的最大值为
的最大值为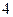 ,求a的值,并说明此时
,求a的值,并说明此时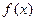 的图象可由函数
的图象可由函数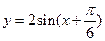 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?
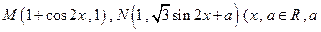 是常数
是常数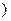 ,令
,令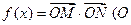 是坐标原点
是坐标原点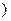 .
.(Ⅰ)求函数
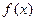 的解析式,并求函数
的解析式,并求函数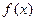 在
在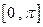 上的单调递增区间;
上的单调递增区间;(Ⅱ)当
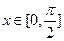 时,
时,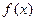 的最大值为
的最大值为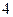 ,求a的值,并说明此时
,求a的值,并说明此时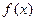 的图象可由函数
的图象可由函数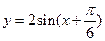 的图象经过怎样的平移和伸缩变换而得到?
的图象经过怎样的平移和伸缩变换而得到?(Ⅰ)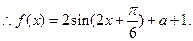 递增区间为
递增区间为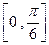 和
和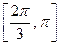
(Ⅱ)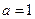
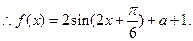 递增区间为
递增区间为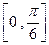 和
和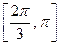
(Ⅱ)
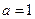
(Ⅰ)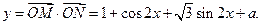
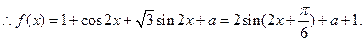
由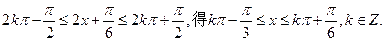
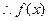 在
在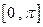 上的单调递增区间为
上的单调递增区间为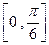 和
和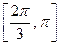 .
.
(Ⅱ)
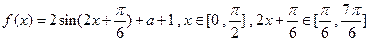 ,
,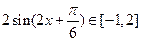 ,
,
∴当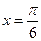 时,
时,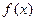 取最大值
取最大值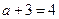 ,解得
,解得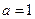 ,∴
,∴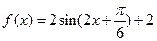 .
.
将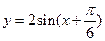 的图象的每一点的横坐标缩短到原来的一半,纵坐标保持不变,再向上平移2个单位长度,得
的图象的每一点的横坐标缩短到原来的一半,纵坐标保持不变,再向上平移2个单位长度,得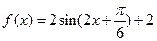 的图象.
的图象.
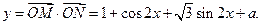
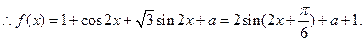
由
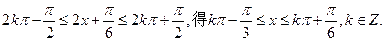
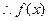 在
在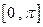 上的单调递增区间为
上的单调递增区间为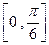 和
和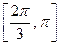 .
.(Ⅱ)
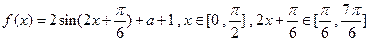 ,
,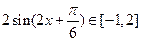 ,
,∴当
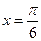 时,
时,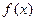 取最大值
取最大值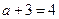 ,解得
,解得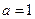 ,∴
,∴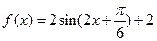 .
.将
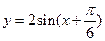 的图象的每一点的横坐标缩短到原来的一半,纵坐标保持不变,再向上平移2个单位长度,得
的图象的每一点的横坐标缩短到原来的一半,纵坐标保持不变,再向上平移2个单位长度,得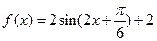 的图象.
的图象.
练习册系列答案
相关题目
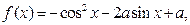 在区间
在区间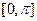 上有最小值
上有最小值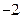 ,求
,求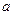 的值.
的值.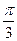 ―2x),
―2x),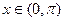 的单调增区间
的单调增区间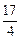 ,求a的取值范围。
,求a的取值范围。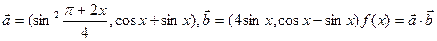
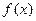 的解析式
的解析式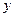 轴的正半轴及
轴的正半轴及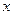 轴的正半轴三者围成图形的面积
轴的正半轴三者围成图形的面积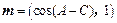 和
和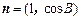 满足
满足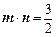 .
.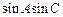 的值;
的值;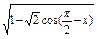 的定义域和值域.
的定义域和值域.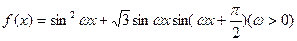
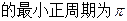 (1)求
(1)求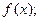
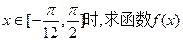 的值域。
的值域。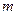 的值;
的值; 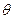 的值
的值