摘要：①当时.△QAP∽△ABC.则有.求得t=1.2(秒)
网址：http://m.1010jiajiao.com/timu_id_450650[举报]
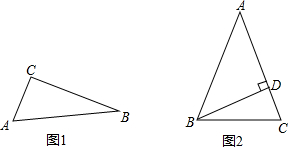（1）在三角形ABC中，∠C=90°，则有AB2=AC2+BC2．例如：当AC=6，BC=8，∠C=90°时，AB2=62+82=100，∴AB=10（如图1），根据上述方法解下题：现已知x轴上一点M（3，0），y轴上一点N（0，-4），连接MN．
求：①MN的长；
②求△MON的面积．
（2）如图2，△ABC中，∠ABC=∠C=2∠A，且BD⊥AC于D．求∠DBC的度数．
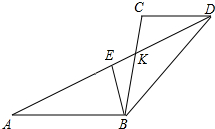如图，已知线段AB∥CD，AD与BC相交于点K，E是线段AD上一动点．（1）若BK=
| 5 |
| 2 |
| CD |
| AB |
（2）连接BE，若BE平分∠ABC，则当AE=
| 1 |
| 2 |
| 1 |
| n |
如图1，在△ABC中，E、D分别为AB、AC上的点，且ED∥BC，O为DC中点，连结EO并延长交BC的延长线于点F，则有S四边形EBCD=S△EBF．
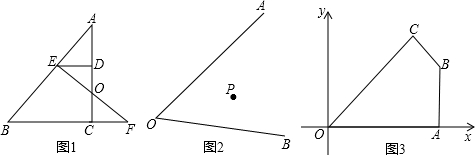
（1）如图2，在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．将直线MN绕着点P旋转的过程中发现，当直线MN满足某个条件时，△MON的面积存在最小值．直接写出这个条件： ．
（2）如图3，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3）、（
，
）、（4、2），过点P的直线l与四边形OABC一组对边相交，将四边形OABC分成两个四边形，求其中以点O为顶点的四边形面积的最大值．
查看习题详情和答案>>
（1）如图2，在已知锐角∠AOB内有一个定点P．过点P任意作一条直线MN，分别交射线OA、OB于点M、N．将直线MN绕着点P旋转的过程中发现，当直线MN满足某个条件时，△MON的面积存在最小值．直接写出这个条件：
（2）如图3，在平面直角坐标系中，O为坐标原点，点A、B、C、P的坐标分别为（6，0）、（6，3）、（
| 9 |
| 2 |
| 9 |
| 2 |
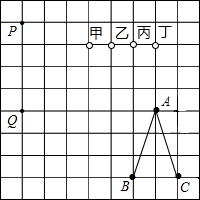如图，棋盘上有A、B、C三个黑子和P、Q两个白子，若使△RPQ∽△ABC，则第三个白子R应该放在（ ）