题目内容
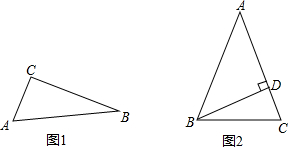 (1)在三角形ABC中,∠C=90°,则有AB2=AC2+BC2.例如:当AC=6,BC=8,∠C=90°时,AB2=62+82=100,∴AB=10(如图1),根据上述方法解下题:
(1)在三角形ABC中,∠C=90°,则有AB2=AC2+BC2.例如:当AC=6,BC=8,∠C=90°时,AB2=62+82=100,∴AB=10(如图1),根据上述方法解下题:现已知x轴上一点M(3,0),y轴上一点N(0,-4),连接MN.
求:①MN的长;
②求△MON的面积.
(2)如图2,△ABC中,∠ABC=∠C=2∠A,且BD⊥AC于D.求∠DBC的度数.
分析:(1)根据题意画出图形,然后利用勾股定理直接求出MN的值,再利用三角形的面积公式求解即可;
(2)根据三角形的内角和定理与∠ABC=∠C=2∠A,即可求得△ABC三个内角的度数,再根据直角三角形的两个锐角互余求得∠DBC的度数.
(2)根据三角形的内角和定理与∠ABC=∠C=2∠A,即可求得△ABC三个内角的度数,再根据直角三角形的两个锐角互余求得∠DBC的度数.
解答:解:(1)根据题意画出图形如下所示:
①MN=
=
=5;
②S△MON=
×3×4=6.
(2)∵∠ABC=∠C=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°-∠C=18°.
①MN=
| OM2+ON2 |
| 32+42 |
②S△MON=
| 1 |
| 2 |
(2)∵∠ABC=∠C=2∠A,
∴∠C+∠ABC+∠A=5∠A=180°,
∴∠A=36°.
则∠C=∠ABC=2∠A=72°.
又BD是AC边上的高,
则∠DBC=90°-∠C=18°.
点评:本题考查了勾股定理、三角形的面积公式及三角形内角和定理的运用,注意掌握三角形的内角和是180°,属于基础题,比价容易解答.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
 任意一个三角形,如图所示,在三角形ABC中取各边中点依次为D、E、F,连接D、E、EF、FD得到三角形DEF,回答下列问题:
任意一个三角形,如图所示,在三角形ABC中取各边中点依次为D、E、F,连接D、E、EF、FD得到三角形DEF,回答下列问题: 如图,点P在三角形ABC的边BC上.
如图,点P在三角形ABC的边BC上. 请你在横线上补充完整其推理过程或理由.
请你在横线上补充完整其推理过程或理由. 如图,已知在三角形ABC中,角BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,求证:BN=CM.
如图,已知在三角形ABC中,角BAC的平分线与BC的垂直平分线PQ相交于点P,过点P分别作PN垂直于AB于点N,PM垂直于AC于点M,求证:BN=CM.