摘要:3.引出反函数的概念(只让学生理解.加宽学生视野) 当一个函数是一一映射时.可以把这个函数的因变量作为一个新的函数自变量.而把这个函数的自变量作为新的函数的因变量.我们称这两个函数为反函数. 由反函数的概念可知.同底的指数函数和对数函数互为反函数. 如的反函数.但习惯上.通常以表示自变量.表示函数.对调中的.这样是指数函数的反函数. 以后.我们所说的反函数是对调后的函数.如的反函数是. 同理.>1)的反函数是>0且. 课堂练习:求下列函数的反函数 (1) (2) 归纳小结: 1. 今天我们主要学习了什么?
网址:http://m.1010jiajiao.com/timu_id_4460293[举报]
(2013•闸北区一模)假设你已经学习过指数函数的基本性质和反函数的概念,但还没有学习过对数的相关概念.由指数函数f(x)=ax(a>0且a≠1)在实数集R上是单调函数,可知指数函数f(x)=ax(a>0且a≠1)存在反函数y=f-1(x),x∈(0,+∞).请你依据上述假设和已知,在不涉及对数的定义和表达形式的前提下,证明下列命题:
(1)对于任意的正实数x1,x2,都有f-1(x1x2)=f-1(x1)+f-1(x2);
(2)函数y=f-1(x)是单调函数.
查看习题详情和答案>>
(1)对于任意的正实数x1,x2,都有f-1(x1x2)=f-1(x1)+f-1(x2);
(2)函数y=f-1(x)是单调函数.
假设你已经学习过指数函数的基本性质和反函数的概念,但还没有学习过对数的相关概念.由指数函数f(x)=ax(a>0且a≠1)在实数集R上是单调函数,可知指数函数f(x)=ax(a>0且a≠1)存在反函数y=f-1(x),x∈(0,+∞).请你依据上述假设和已知,在不涉及对数的定义和表达形式的前提下,证明下列命题:
(1)对于任意的正实数x1,x2,都有f-1(x1x2)=f-1(x1)+f-1(x2);
(2)函数y=f-1(x)是单调函数.
查看习题详情和答案>>
(1)对于任意的正实数x1,x2,都有f-1(x1x2)=f-1(x1)+f-1(x2);
(2)函数y=f-1(x)是单调函数.
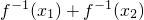 ;
; ;
;