题目内容
假设你已经学习过指数函数的基本性质和反函数的概念,但还没有学习过对数的相关概念.由指数函数f(x)=ax(a>0且a≠1)在实数集R上是单调函数,可知指数函数f(x)=ax(a>0且a≠1)存在反函数y=f-1(x),x∈(0,+∞).请你依据上述假设和已知,在不涉及对数的定义和表达形式的前提下,证明下列命题:
(1)对于任意的正实数x1,x2,都有f-1(x1x2)=f-1(x1)+f-1(x2);
(2)函数y=f-1(x)是单调函数.
(1)对于任意的正实数x1,x2,都有f-1(x1x2)=f-1(x1)+f-1(x2);
(2)函数y=f-1(x)是单调函数.
证明:(1)设y1=f-1(x1),y2=f-1(x2),
由题意,有x1=ay1,x2=ay2,
∴x1x2=ay1•ay2=ay1+y2,
∴y1+y2=f-1(x1x2),即f-1(x1x2)=f-1(x1)+f-1(x2).
(2)当a>1时,y=f-1(x)是增函数.
证明:设x1>x2>0,即ay1>a y2>0,
又由指数函数y=ax(a>1)是增函数,得y1>y2,即f-1(x1)>f-1(x2).
∴当a>1时,y=f-1(x)是增函数.
同理,当0<a<1时,y=logax是减函数.
由题意,有x1=ay1,x2=ay2,
∴x1x2=ay1•ay2=ay1+y2,
∴y1+y2=f-1(x1x2),即f-1(x1x2)=f-1(x1)+f-1(x2).
(2)当a>1时,y=f-1(x)是增函数.
证明:设x1>x2>0,即ay1>a y2>0,
又由指数函数y=ax(a>1)是增函数,得y1>y2,即f-1(x1)>f-1(x2).
∴当a>1时,y=f-1(x)是增函数.
同理,当0<a<1时,y=logax是减函数.

练习册系列答案
相关题目
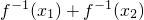 ;
; ;
;