摘要：9．求二次函数的最值问题时你注意到x的取值范围了吗?“方程有实数解 转化为“ .你是否注意到“ (除解决二次方程的有关问题时要注意之外.在解决直线与圆锥曲线的位置关系时.也常常遇到).在题目中没有指出是“二次 函数.方程.不等式时.就要分类讨论的不同情况.不要忽略的讨论.
网址：http://m.1010jiajiao.com/timu_id_4419486[举报]
（2006•宝山区二模）给出函数f(x)=
+tx（x∈R）．
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
时，可以将f（x）化成f(x)=a(
+x)+b(
-x)的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
+h(x)，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
| x2+4 |
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
| 1 |
| 2 |
| x2+4 |
| x2+4 |
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
| g(x) |
给出函数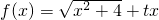
（x∈R）
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当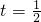
时，可以将f（x）化成
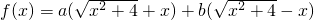的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记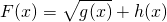
，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
关于二次函数学生甲有以下观点：①二次函数必有最大值；②二次函数必有最小值；③闭区间上的二次函数必定同时存在最大值，最小值；④对于命题③，最值一定在区间端点取得．你认为学生甲正确的观点序号是 ．根据你的判断试解决下述问题：已知函数f（x）=ax2+（2a-1）x+1在[-
，2]上的最大值为3，求实数a的值．
查看习题详情和答案>>
| 3 | 2 |
（t∈R）有最大值且最大值为正实数，集合
，集合B={x|x2＜b2}。
B}，P（E）为x取自A-B的概率，P（F）为x取自A∩B的概率，解答下面问题：
，P（F）=
。