题目内容
给出函数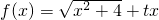 (x∈R)
(x∈R)
(1)当t≤-1时,证明y=f(x)是单调递减函数;
(2)当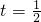 时,可以将f(x)化成
时,可以将f(x)化成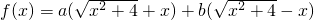 的形式,运用基本不等式求f(x)的最小值及此时x的取值;
的形式,运用基本不等式求f(x)的最小值及此时x的取值;
(3)设一元二次函数g(x)的图象均在x轴上方,h(x)是一元一次函数,记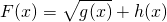 ,利用基本不等式研究函数F(x)的最值问题.
,利用基本不等式研究函数F(x)的最值问题.
解:(1)设x1<x2,则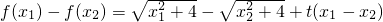
化成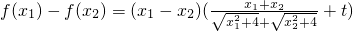
显然,当x1+x2≤0时,f(x1)-f(x2)>0
当x1+x2>0时,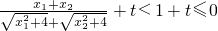 ,即f(x1)-f(x2)>0
,即f(x1)-f(x2)>0
所以y=f(x)是单调递减函数;
(2)由题意得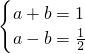 ,解得
,解得 ,
,
∴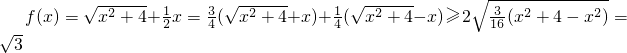
当且仅当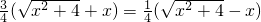 ,即
,即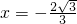 时,
时, ;
;
(3)由题意设g(x)=a(x-m)2+n,(a>0,n>0),h(x)=tx+b (t≠0),
所以 .
.
若用x代换x-m,用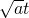 代换t,则F(x)总能化成
代换t,则F(x)总能化成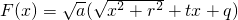 (r>0)的形式.
(r>0)的形式.
由于 及q均是常数,因而,只需研究
及q均是常数,因而,只需研究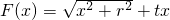 (r>0)的最值.
(r>0)的最值.
当|t|≥1时,F(x)是单调函数,无最值.
当|t|<1时,
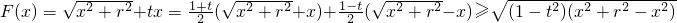
即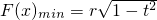 ,此时
,此时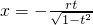 .
.
分析:(1)设x1<x2,对应的函数值作差后化为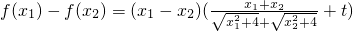 ,分x1+x2≤0和x1+x2>0判断查实的符号,从而得到结论;
,分x1+x2≤0和x1+x2>0判断查实的符号,从而得到结论;
(2)把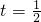 代入,由题意得到关于a,b的二元一次方程组,求出a,b的值,然后直接利用基本不等式求最值;
代入,由题意得到关于a,b的二元一次方程组,求出a,b的值,然后直接利用基本不等式求最值;
(3)设出两个函数g(x)和h(x)的解析式,得到F(x)后用x代换x-m,用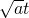 代换t,则F(x)总能化成
代换t,则F(x)总能化成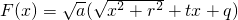 (r>0)的形式,分|t|大于等于1及小于1讨论最值情况.
(r>0)的形式,分|t|大于等于1及小于1讨论最值情况.
点评:本题考查了函数单调性的判断与证明,训练了利用基本不等式求函数的最值,考查了学生灵活处理和解决问题的能力,考查了数学转化思想方法,是有一定难度题目.
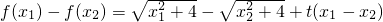
化成
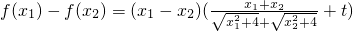
显然,当x1+x2≤0时,f(x1)-f(x2)>0
当x1+x2>0时,
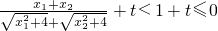 ,即f(x1)-f(x2)>0
,即f(x1)-f(x2)>0所以y=f(x)是单调递减函数;
(2)由题意得
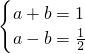 ,解得
,解得 ,
,∴
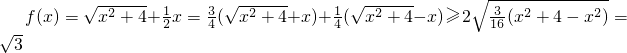
当且仅当
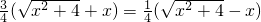 ,即
,即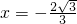 时,
时, ;
;(3)由题意设g(x)=a(x-m)2+n,(a>0,n>0),h(x)=tx+b (t≠0),
所以
 .
.若用x代换x-m,用
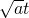 代换t,则F(x)总能化成
代换t,则F(x)总能化成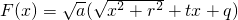 (r>0)的形式.
(r>0)的形式.由于
 及q均是常数,因而,只需研究
及q均是常数,因而,只需研究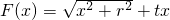 (r>0)的最值.
(r>0)的最值.当|t|≥1时,F(x)是单调函数,无最值.
当|t|<1时,
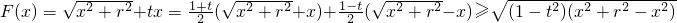
即
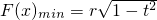 ,此时
,此时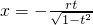 .
.分析:(1)设x1<x2,对应的函数值作差后化为
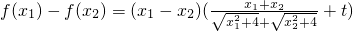 ,分x1+x2≤0和x1+x2>0判断查实的符号,从而得到结论;
,分x1+x2≤0和x1+x2>0判断查实的符号,从而得到结论;(2)把
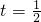 代入,由题意得到关于a,b的二元一次方程组,求出a,b的值,然后直接利用基本不等式求最值;
代入,由题意得到关于a,b的二元一次方程组,求出a,b的值,然后直接利用基本不等式求最值;(3)设出两个函数g(x)和h(x)的解析式,得到F(x)后用x代换x-m,用
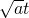 代换t,则F(x)总能化成
代换t,则F(x)总能化成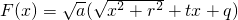 (r>0)的形式,分|t|大于等于1及小于1讨论最值情况.
(r>0)的形式,分|t|大于等于1及小于1讨论最值情况.点评:本题考查了函数单调性的判断与证明,训练了利用基本不等式求函数的最值,考查了学生灵活处理和解决问题的能力,考查了数学转化思想方法,是有一定难度题目.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目