题目内容
已知二次函数f(t)=at2-| b |
| 1 |
| 4a |
|
|
(1)求A和B;
(2)定义A与B的差集:A-B=
|
①当a=-3,b=2时,求P(E),P(F)取值?
②设a,b,x均为整数时,写出a与b的三组值,使P(E)=
| 2 |
| 3 |
| 1 |
| 3 |
分析:(1)先函数f(t)进行配方,根据函数f(t)的最大值为正实数可确定b的范围,然后分别求出集合A和集合B即可;
(2)①P(E)=
;P(F)=
②要使P(E)=
,P(F)=
.可以分三种情形考虑:A中有3个元素,A-B中有2个元素,A∩B中有1个元素;A中有6个元素,A-B中有4个元素,A∩B中有2个元素;A中有9个元素,A-B中有6个元素,A∩B中有3个元素,分别求得a,b即可.
(2)①P(E)=
| 1 |
| 3 |
| 2 |
| 3 |
②要使P(E)=
| 2 |
| 3 |
| 1 |
| 3 |
解答:解:(1)∵f(t)=at2-
t+
(t∈R),
配方得 f(t)=a(t-
)2+
,
由a<0得最大值
>0?b>1.
∴A={x|a<x<0},B={x|-b<x<b}.
(2)①P(E)=
;P(F)=
②要使P(E)=
,P(F)=
.可以使:
A中有3个元素,A-B中有2个元素,A∩B中有1个元素.a=-4,b=2.
A中有6个元素,A-B中有4个元素,A∩B中有2个元素.则a=-7,b=3.
A中有9个元素,A-B中有6个元素,A∩B中有3个元素.则a=-10,b=4.
| b |
| 1 |
| 4a |
配方得 f(t)=a(t-
| ||
| 2a |
| 1-b |
| 4b |
由a<0得最大值
| 1-b |
| 4a |
∴A={x|a<x<0},B={x|-b<x<b}.
(2)①P(E)=
| 1 |
| 3 |
| 2 |
| 3 |
②要使P(E)=
| 2 |
| 3 |
| 1 |
| 3 |
A中有3个元素,A-B中有2个元素,A∩B中有1个元素.a=-4,b=2.
A中有6个元素,A-B中有4个元素,A∩B中有2个元素.则a=-7,b=3.
A中有9个元素,A-B中有6个元素,A∩B中有3个元素.则a=-10,b=4.
点评:本题主要考查了函数的最值及其几何意义,以及分段函数和古典概型及其概率计算公式,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
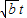 +
+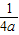 (t∈R)有最大值且最大值为正实数,集合A=
(t∈R)有最大值且最大值为正实数,集合A=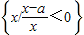 ,集合B=
,集合B=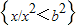 .
.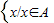 且x∉B.且x∈A.P(E)为x取自A-B的概率.P(F)为x取自A/B的概率.解答下面问题:
且x∉B.且x∈A.P(E)为x取自A-B的概率.P(F)为x取自A/B的概率.解答下面问题: ,P(F)=
,P(F)= .
.