题目内容
关于二次函数学生甲有以下观点:①二次函数必有最大值;②二次函数必有最小值;③闭区间上的二次函数必定同时存在最大值,最小值;④对于命题③,最值一定在区间端点取得.你认为学生甲正确的观点序号是| 3 | 2 |
分析:(1)二次函数在开区间上可能没有最大值和最小值,故①②不正确,而④的情况下,若区间中包含对称轴,则最值不一定在区间端点取得,故④错,③正确.
(2)首先要讨论a的取值情况.当a=0时,f(x)为单减的一次函数,易得a的值;当a≠0时,考虑对称轴的问题,分情况计算,即可得到答案.
(2)首先要讨论a的取值情况.当a=0时,f(x)为单减的一次函数,易得a的值;当a≠0时,考虑对称轴的问题,分情况计算,即可得到答案.
解答:解:(1)二次函数在开区间上可能没有最大值和最小值,如y=x2在(1,3)上既没有最大值,也没有最小值,则①、②均错误,
由函数的最值定理,可得③正确,
对于④,其区间若包含对称轴,则最值不一定在区间端点取得,故④错,(2分)
(2)当a=0时,f(x)=-x+1在[-
,2]上的最大值为
f(-
) =
≠3不合题意,舍去;(3分)
当a≠0时,
①令f(-
) =3得a=-
,此时抛物线开口向下,对称轴x=-2,
且-2∉[-
,2],故a= -
不合题意,舍去;(6分)
②令f(2)=3,得a=
,此时抛物线开口向上,
闭区间的右端点距离对称轴较远,故a=
符合题意;(9分)
③若f(-
) =3得a=-
经检验符合题意,(12分)
综上可知:实数a的值为a=
或a=-
(13分)
由函数的最值定理,可得③正确,
对于④,其区间若包含对称轴,则最值不一定在区间端点取得,故④错,(2分)
(2)当a=0时,f(x)=-x+1在[-
| 3 |
| 2 |
f(-
| 3 |
| 2 |
| 5 |
| 2 |
当a≠0时,
①令f(-
| 2a-1 |
| 2a |
| 1 |
| 2 |
且-2∉[-
| 3 |
| 2 |
| 1 |
| 2 |
②令f(2)=3,得a=
| 1 |
| 2 |
闭区间的右端点距离对称轴较远,故a=
| 1 |
| 2 |
③若f(-
| 3 |
| 2 |
| 2 |
| 3 |
综上可知:实数a的值为a=
| 1 |
| 2 |
| 2 |
| 3 |
点评:此题主要考查二次函数的单调性和相关性质.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
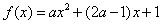 在
在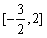 上的最大值为3,求实数a的值。
上的最大值为3,求实数a的值。 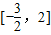 上的最大值为3,求实数a的值.
上的最大值为3,求实数a的值.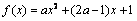 在
在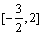 上的最大值为3, 求实数a的值.
上的最大值为3, 求实数a的值.