摘要：19．(Ⅰ)证明:如图.连结B1C交BC1于F.连结DE.DF.则由题设可知:EF 而A1D ∴EFA1D∴四边形A1DFE为平行四边形.∴A1E//DF.又DF平面DBC1.A1E面DBC1. ∴A1E//面DBC1. 取BC的中点F.连结EF交BC1于点O.则O为BC1的中点. 过M作MN//A1E交OE于点N.则. ∵A1E⊥面B1BCC1. ∴MN⊥面B1BCC1. ∴过N作NR⊥BC1交BC1于R.连结MR.则∠MRN为二面角M-BC1-B1的平面角. 要使 显然说明点M在AA1的延长线上.同理.在A1A的延长线上也存在一点P.得. 在A1A所在直线上存在点M.使二面角M-BC1-B1成60°.且AP=2+或 .过E作EP⊥BC1.连结A1P. 由题意知.∽
网址：http://m.1010jiajiao.com/timu_id_4419020[举报]
如图，F1，F2是椭圆| x2 |
| a2 |
| y2 |
| b2 |
（1）求椭圆的离心率e
（2）若Q是椭圆上任意一点，证明∠F1QF2≤
| π |
| 2 |
（3）过F1与OP垂直的直线交椭圆于M，N，若△M F2N的面积为20
| 3 |
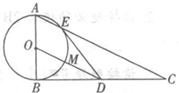
4-1（几何证明选讲）如图，△ABC是直角三角形，∠ABC=90o．以AB为直径的圆0交AC于点E点D是BC边的中点，连0D交圆0于点M
（I）求证：0，B，D，E四点共圆；
（II）求证：2DE2=DM•AC+DM•AB 查看习题详情和答案>>
如图，三角形PAB是半圆锥PO的一个轴截面，PO=1，AB=2，四棱锥P-ABCD的底面为正方形，且与圆锥PO的底面共面．（Ⅰ）若H为圆锥PO的底面半圆周上的一点，且BH∥OC，连AH，证明：AH⊥PC；
（Ⅱ）在圆锥PO的底面半圆周上确定点G的位置，使母线PG与平面PCD所成角的正弦值为
| ||
| 4 |
（2004•上海模拟）如图，⊙O半径为2，直径CD以O为中心，在⊙O所在平面内转动，当CD 转动时，OA固定不动，0°≤∠DOA≤90°，且总有BC∥OA，AB∥CD，若OA=4，BC与⊙O交于E，连AD，设CE为x，四边形ABCD的面积为y．
A．（不等式选做题）不等式|x-1|+|x+2|＜a的解集不是空集，则实数a的取值范围为