题目内容
 A.(不等式选做题)不等式|x-1|+|x+2|<a的解集不是空集,则实数a的取值范围为
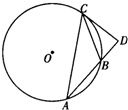
A.(不等式选做题)不等式|x-1|+|x+2|<a的解集不是空集,则实数a的取值范围为B.(几何证明选做题)如图,割线PBC经过圆心O,OB=PB=1,OB绕点O逆时针旋转120°到OD,连PD交圆O于点E,则PE=
C.(极坐标系与参数方程选做题)在极坐标系中,已知曲线p=2cosθ与直线3ρcosθ+4ρsinθ+a=0相切,则实数a的值为
分析:A,利用绝对值不等式的性质:|a|+|b|≥|a+b|(当且仅当a与b同号取等号),求出原不等式左边的最小值,让a大于等于求出的最小值,即可得到满足题意的实数a的取值范围.
B,先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
C,先圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.
B,先由余弦定理求出PD,再根据割线定理即可求出PE,问题解决.
C,先圆ρ=2cosθ与直线3ρcosθ+4ρsinθ+a=0,利用直角坐标与极坐标间的关系,即利用ρcosθ=x,ρsinθ=y,ρ2=x2+y2,进行代换即得直角坐标系,再利用直角坐标方程求解即可.
解答:解:A:∵|x+2|+|x-1|=|x+2|+|1-x|≥|x+2+1-x|=3,
∴|x+2|+|x-3|的最小值为3,
又不等式|x+2|+|x-3|≤a的解集不是空集,
∴a≥3.
故答案为:(3,+∞);
B:由余弦定理得,PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2×(-
)=7,
所以PD=
.
根据割线定理PE•PD=PB•PC得,
PE=1×3,
所以PE=
.
故答案为
.
C:p2=2pcosθ,圆ρ=2cosθ的普通方程为:x2+y2=2x,(x-1)2+y2=1,
直线3ρcosθ+4ρsinθ+a=0的普通方程为:3x+4y+a=0,
又圆与直线相切,所以
=1,解得:a=2,或a=-8.
故答案为:a=2或a=-8
∴|x+2|+|x-3|的最小值为3,
又不等式|x+2|+|x-3|≤a的解集不是空集,
∴a≥3.
故答案为:(3,+∞);
B:由余弦定理得,PD2=OD2+OP2-2OD•OPcos120°=1+4-2×1×2×(-
| 1 |
| 2 |
所以PD=
| 7 |
根据割线定理PE•PD=PB•PC得,
| 7 |
所以PE=
3
| ||
| 7 |
故答案为
3
| ||
| 7 |
C:p2=2pcosθ,圆ρ=2cosθ的普通方程为:x2+y2=2x,(x-1)2+y2=1,
直线3ρcosθ+4ρsinθ+a=0的普通方程为:3x+4y+a=0,
又圆与直线相切,所以
| |3•1+4•0+a| | ||
|
故答案为:a=2或a=-8
点评:A:此题考查绝对值不等式的性质及其解法,这类题目是高考的热点,难度不是很大,要注意不等号进行放缩的方向.B:已知三角形两边与夹角时,一定要想到余弦定理的运用,之后做题的思路也许会豁然开朗.C:本题主要考查曲线的极坐标方程等基本知识,考查转化问题的能力.

练习册系列答案
相关题目
 A.(不等式选做题)
A.(不等式选做题)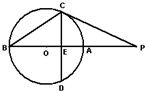 A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
A.(不等式选做题)不等式|3x-6|-|x-4|>2x的解集为
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评分) 选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)
选做题:(考生注意:请在下列三题中任选一题作答,如果多做,则按所做第一题评分)