��Ŀ����
 ��2004•�Ϻ�ģ�⣩��ͼ����O�뾶Ϊ2��ֱ��CD��OΪ���ģ��ڡ�O����ƽ����ת������CD ת��ʱ��OA�̶�������0��ܡ�DOA��90�㣬������BC��OA��AB��CD����OA=4��BC���O����E����AD����CEΪx���ı���ABCD�����Ϊy��
��2004•�Ϻ�ģ�⣩��ͼ����O�뾶Ϊ2��ֱ��CD��OΪ���ģ��ڡ�O����ƽ����ת������CD ת��ʱ��OA�̶�������0��ܡ�DOA��90�㣬������BC��OA��AB��CD����OA=4��BC���O����E����AD����CEΪx���ı���ABCD�����Ϊy����1����y����x�ĺ�������ʽ����ָ��x��ȡֵ��Χ��
��2����x=2
| 3 |
��4����xȡ��ֵʱ���ı���ABCDΪֱ�����Σ���EF����ʱOCEF���ʲôͼ�Σ���ֻ��˵�����ۣ�����֤������
��������1�������ı���ABCD���ǹ�����ı��Σ��ɽ���ֳ�ƽ���ı���ABCO�͡�AOD����������⣬����DE����O��OH��BC��H����ô���ѵó�OH�ǡ�CDE����λ�ߣ���ֱ��������CDE�У�����ֱ����CE�ij����DE��ֵ��Ȼ�ɵó�OH�ij��������ɸ����ı���ABCD��������㷽�����y��x�ĺ�����ϵʽ������˵x��ȡֵ��Χ��0��ܡ�DOA��90�㣻���0��cos��DOA��1����cos��DOA=
=
����0��
��1����0��x��4��
��2������OE����ô�ı��ε�Բ�ڲ��ֿɷ�Ϊ����ODE�͡�OCE�����֣���OCE�����������ã��ص�˵������ODE��������㷽�����ؼ������Բ�Ľǡ�DOE�Ķ�������ֱ��������CDE�У�CD=4��CE=2
����ˡ�DCE=30�㣻����Բ�ܽǶ�������DOE=2��DCE=60�㣻�������ε������ʽ�����������ODE�������Ȼ���ٷֱ�������OCE��������ı���ABCD����������бȽϼ��ɣ�
��3�����ı���ABCD��ֱ������ʱ��CD��AB��CD��AB����BC��ֱ����ʱC��E�غϣ�CE=x=0�����OCEF����˵���ֱ�������Σ�
| CE |
| CD |
| x |
| 4 |
| x |
| 4 |
��2������OE����ô�ı��ε�Բ�ڲ��ֿɷ�Ϊ����ODE�͡�OCE�����֣���OCE�����������ã��ص�˵������ODE��������㷽�����ؼ������Բ�Ľǡ�DOE�Ķ�������ֱ��������CDE�У�CD=4��CE=2
| 3 |
��3�����ı���ABCD��ֱ������ʱ��CD��AB��CD��AB����BC��ֱ����ʱC��E�غϣ�CE=x=0�����OCEF����˵���ֱ�������Σ�
����⣺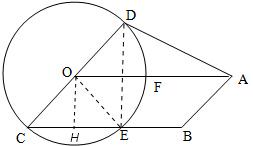 ��1������DE����O��OH��BC��H����DE��BC��OH��DE
��1������DE����O��OH��BC��H����DE��BC��OH��DE
��CD=4��CE=x
��DE=
=
=
��OH=
DE=
��y=S?ABCO+S��OAD=4��
+
��4��
=3
��0��x��4��
��x��ȡֵ��ΧΪ0��x��4��
��2����x=2
ʱ
��CE=2
��CD=4
��DE=2����C=30��
���DOE=60�㣬OH=1
��SԲ�ڲ���=
+
��2
��1=
+
��S�ı���ABCD=3
=3
=6
��SԲ�ڲ�����S�ı���ABCD=
���ı���ABCD��Բ�ڵ�������ı���ABCD�����֮��Ϊ��2��+3
����18��
��3��x=0ʱ��E��C�غϣ��ı���ABCDΪֱ�����Σ�OCEF��������OCF����״�ǵ���ֱ�������Σ�
��x=2ʱ��CD��AB����AD��ֱ��
 ��1������DE����O��OH��BC��H����DE��BC��OH��DE
��1������DE����O��OH��BC��H����DE��BC��OH��DE��CD=4��CE=x
��DE=
| CD2-CE2 |
| 42-x2 |
| 16-x2 |
��OH=
| 1 |
| 2 |
| ||
| 2 |
��y=S?ABCO+S��OAD=4��
| ||
| 2 |
| 1 |
| 2 |
| ||
| 2 |
=3
| 16-x2 |
��x��ȡֵ��ΧΪ0��x��4��
��2����x=2
| 3 |
��CE=2
| 3 |
��DE=2����C=30��
���DOE=60�㣬OH=1
��SԲ�ڲ���=
| 60����22 |
| 360 |
| 1 |
| 2 |
| 3 |
| 2�� |
| 3 |
| 3 |
��S�ı���ABCD=3
| 16-x2 |
| 16-12 |
��SԲ�ڲ�����S�ı���ABCD=
2��+3
| ||
| 18 |
���ı���ABCD��Բ�ڵ�������ı���ABCD�����֮��Ϊ��2��+3
| 3 |
��3��x=0ʱ��E��C�غϣ��ı���ABCDΪֱ�����Σ�OCEF��������OCF����״�ǵ���ֱ�������Σ�
��x=2ʱ��CD��AB����AD��ֱ��
������������Ҫ������Բ�ܽǶ�����ƽ���ı��ε����ʡ�ͼ������������Ǻ�����ֱ�����ε��ж���֪ʶ����ۺ�����������

��ϰ��ϵ�д�
�����Ŀ