题目内容
 如图,F1,F2是椭圆
如图,F1,F2是椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆的离心率e
(2)若Q是椭圆上任意一点,证明∠F1QF2≤
| π |
| 2 |
(3)过F1与OP垂直的直线交椭圆于M,N,若△M F2N的面积为20
| 3 |
分析:(1)根据题意可表示出MP坐标,进而表示出直线OP的斜率和AB的斜率利用二者相等求得b和c的关系进而求得a和c的关系,则离心率可得.
(2)利用椭圆的定义可表示出|F1Q|+|F2Q|,进而利用余弦定理表示出cos∠F1QF2,利用基本不等式可得cos∠F1QF2的范围进而求得∠F1QF2的范围.
(3)设出直线MN的方程,代入椭圆方程消去x整理后利用韦达定理表示出y1+y2和y1•y2,进而求得|y1-y2|代入三角形面积公式求得求得c,进而可分别求得a和b,则椭圆的方程可得.
(2)利用椭圆的定义可表示出|F1Q|+|F2Q|,进而利用余弦定理表示出cos∠F1QF2,利用基本不等式可得cos∠F1QF2的范围进而求得∠F1QF2的范围.
(3)设出直线MN的方程,代入椭圆方程消去x整理后利用韦达定理表示出y1+y2和y1•y2,进而求得|y1-y2|代入三角形面积公式求得求得c,进而可分别求得a和b,则椭圆的方程可得.
解答:解:(1)易得 P(-c,
),kOP=
,kAB=-
,
∴-
=-
⇒b=c⇒a=
c,
∴e=
=
.
(2)证明:由椭圆定义得:|F1Q|+|F2Q|=2a,
所以cos∠F1QF2=
=
=
-1,
因为|F1Q||F2Q|≤(
)2=a2,
∴cos∠F1QF2≥
-1=
-1=0,
∴∠F1QF2≤
.
(3)解:设直线MN的方程为 y=
(x+c),即y=
(x+c).
代入椭圆方程消去x得:
+
=1,
整理得:5y2-2
cy-2c2=0,
∴y1+y2=
,y1•y2=-
.
∴(y1-y2)2=(
)2+
=
.
因为S△PF2Q=
•2c•|y1-y2|=
=20
,
所以c2=25
因此a2=50,b2=25,
所以椭圆方程为
+
=1.
| b2 |
| a |
| b2 |
| -ac |
| b |
| a |
∴-
| b2 |
| ac |
| b |
| a |
| 2 |
∴e=
| c |
| a |
| ||
| 2 |
(2)证明:由椭圆定义得:|F1Q|+|F2Q|=2a,
所以cos∠F1QF2=
| |F1Q|2+|F2Q|2-|F1F2|2 |
| 2|F1Q||F2Q| |
=
| 4a2-4c2-2|F1Q||F2Q| |
| 2|F1Q||F2Q| |
| 2b2 |
| |F1Q||F2Q| |
因为|F1Q||F2Q|≤(
| |F1Q|+|F2Q| |
| 2 |
∴cos∠F1QF2≥
| 2b2 |
| a2 |
| 2c2 |
| 2c2 |
∴∠F1QF2≤
| π |
| 2 |
(3)解:设直线MN的方程为 y=
| a |
| b |
| 2 |
代入椭圆方程消去x得:
(1-
| ||||
| a2 |
| y2 |
| b2 |
整理得:5y2-2
| 2 |
∴y1+y2=
2
| ||
| 5 |
| 2c2 |
| 5 |
∴(y1-y2)2=(
2
| ||
| 5 |
| 8c2 |
| 5 |
| 48c2 |
| 25 |
因为S△PF2Q=
| 1 |
| 2 |
4
| ||
| 5 |
| 3 |
所以c2=25
因此a2=50,b2=25,
所以椭圆方程为
| x2 |
| 50 |
| y2 |
| 25 |
点评:本题主要考查了椭圆的简单性质,解决直线与圆锥曲线的位置关系一般的思路是将直线与圆锥曲线方程联立,利用韦达定理找突破口.考查了学生综合分析问题和计算能力.

练习册系列答案
相关题目
 (2013•浦东新区二模)(1)设椭圆C1:
(2013•浦东新区二模)(1)设椭圆C1: 如图,F1,F2为椭圆C:
如图,F1,F2为椭圆C: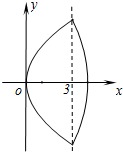 (1)设椭圆C1:
(1)设椭圆C1: 与双曲线C2:
与双曲线C2: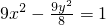 有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;
有相同的焦点F1、F2,M是椭圆C1与双曲线C2的公共点,且△MF1F2的周长为6,求椭圆C1的方程;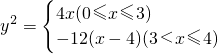 .设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值;
.设“盾圆D”上的任意一点M到F(1,0)的距离为d1,M到直线l:x=3的距离为d2,求证:d1+d2为定值; 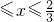 )与第(1)小题椭圆弧E2:
)与第(1)小题椭圆弧E2: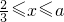 )所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求
)所合成的封闭曲线为“盾圆E”.设过点F(1,0)的直线与“盾圆E”交于A、B两点,|FA|=r1,|FB|=r2且∠AFx=α(0≤α≤π),试用cosα表示r1;并求 的取值范围.
的取值范围.