题目内容
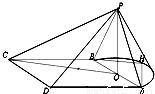
 如图,三角形PAB是半圆锥PO的一个轴截面,PO=1,AB=2,四棱锥P-ABCD的底面为正方形,且与圆锥PO的底面共面.
如图,三角形PAB是半圆锥PO的一个轴截面,PO=1,AB=2,四棱锥P-ABCD的底面为正方形,且与圆锥PO的底面共面.(Ⅰ)若H为圆锥PO的底面半圆周上的一点,且BH∥OC,连AH,证明:AH⊥PC;
(Ⅱ)在圆锥PO的底面半圆周上确定点G的位置,使母线PG与平面PCD所成角的正弦值为
| ||
| 4 |
分析:(Ⅰ)通过H为圆锥PO的底面半圆周上的一点,且BH∥OC,连AH,通过证明PO⊥平面ABCD,说明PO⊥AH利用直线与平面垂直的判定定理证明:AH⊥PC;
(Ⅱ)以O为原点,OA方向为x轴,OP方向为z轴建立空间直角坐标系,求出相关点的坐标,设出平面PCD的一个法向量
,利用
,就是母线PG与平面PCD所成角的正弦值为
,求出G的坐标即可.
(Ⅱ)以O为原点,OA方向为x轴,OP方向为z轴建立空间直角坐标系,求出相关点的坐标,设出平面PCD的一个法向量
| n |
| ||||
|
|
| ||
| 4 |
解答:(本小题满分13分)
解:(Ⅰ)证明:因为H为圆锥PO的底面圆周上的一点,∴AH⊥BH,
又∵BH∥OC,
∴AH⊥OC…(2分)
因为PO⊥平面ABCD,AH?平面ABCD∴PO⊥AH,
∵PO∩OC=O,∴AH⊥平面PCO,…(4分)
∵PC?平面PCO,∴AH⊥PC…(5分)
(Ⅱ)以O为原点,OA方向为x轴,OP方向为z轴建立空间直角坐标系,…(6分)
则P(0,0,1),D(1,-2,0),C(-1,-2,0),
=(1,-2,-1),
=(-1,-2,-1),…(7分)
设平面PCD的一个法向量为
=(x,y,z),则由
得
,
取y=1得平面PCD的一个法向量为
=(0,1,-2);…(9分)
∵G为圆锥PO的底面圆周上的一点,可设G(cosθ,sinθ,0),θ∈[0,π]
=(cosθ,sinθ,-1),依题意得
=
=
,…(11分)
解得sinθ=
,cosθ=±
,
∴点G的坐标为(±
,
,0) …(13分)
解:(Ⅰ)证明:因为H为圆锥PO的底面圆周上的一点,∴AH⊥BH,
又∵BH∥OC,
∴AH⊥OC…(2分)
因为PO⊥平面ABCD,AH?平面ABCD∴PO⊥AH,
∵PO∩OC=O,∴AH⊥平面PCO,…(4分)
∵PC?平面PCO,∴AH⊥PC…(5分)
(Ⅱ)以O为原点,OA方向为x轴,OP方向为z轴建立空间直角坐标系,…(6分)
则P(0,0,1),D(1,-2,0),C(-1,-2,0),
| PD |
| PC |
设平面PCD的一个法向量为
| n |
|
得
|
取y=1得平面PCD的一个法向量为
| n |
∵G为圆锥PO的底面圆周上的一点,可设G(cosθ,sinθ,0),θ∈[0,π]
| PG |
| ||||
|
|
| sinθ+2 | ||||
|
| ||
| 4 |
解得sinθ=
| 1 |
| 2 |
| ||
| 2 |
∴点G的坐标为(±
| ||
| 2 |
| 1 |
| 2 |
点评:本题考查空间几何体中直线与平面垂直的判定定理的应用,直线与平面设出角的求法,空间向量的数量积的应用,考查逻辑推理能力与计算能力.

练习册系列答案
相关题目
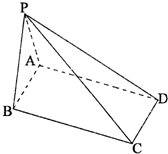 如图,底面是矩形的四棱锥P-ABCD中AB=2,BC=
如图,底面是矩形的四棱锥P-ABCD中AB=2,BC=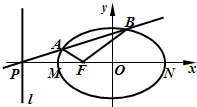 (2008•湖北模拟)如图,设F是椭圆
(2008•湖北模拟)如图,设F是椭圆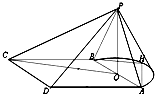 如图,三角形PAB是半圆锥PO的一个轴截面,PO=1,AB=2,四棱锥P-ABCD的底面为正方形,且与圆锥PO的底面共面.
如图,三角形PAB是半圆锥PO的一个轴截面,PO=1,AB=2,四棱锥P-ABCD的底面为正方形,且与圆锥PO的底面共面.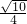 .
. .
.