摘要: (1)解:由题意.有△BEF≌△DEF. ∴BF=DF. --1分 如图.过点A作AG⊥BG于点G. 则四边形AGFD是矩形. ∴AG=DF,GF=AD=4. 在Rt△ABG和Rt△DCF种. ∵AB=DC,AG=DF, ∴Rt△ABG≌Rt△DCF.(HL) ∴BG=CF. --2分 ∴BG===2. ∴DF=BF=BG+GF=2+4=6. --2分 ∴S梯形ABCD=. --1分 (2)猜想:CG=(或). --1分 证明:如图.过点E作EH∥CG,交BC于点H. 则∠FEH=∠FGC. 又∠EFH=∠GFC, ∴△EFH∽△GFC. ∴ 而FG=kEF,即. ∴ 即 --1分 ∵EH∥CG, ∴∠EHB=∠DCB. 而ABCD是等腰梯形.∴∠B=∠DCB. ∴∠B=∠EHB.∴BE=EH. ∴CG= --1分
网址:http://m.1010jiajiao.com/timu_id_4412363[举报]
先阅读然后解答提出的问题:
设a、b是有理数,且满足a+
b=3-2
,求ba的值.
解:由题意得(a-3)+(b+2)
=0,因为a、b都是有理数,所以a-3,b+2也是有理数,由于
是无理数,所以a-3=0,b+2=0,所以a=3,b=-2,所以ba=(-2)3=-8.
问题:设x、y都是有理数,且满足x2-2y+
y=10+3
,求x+y的值.
查看习题详情和答案>>
设a、b是有理数,且满足a+
| 2 |
| 2 |
解:由题意得(a-3)+(b+2)
| 2 |
| 2 |
问题:设x、y都是有理数,且满足x2-2y+
| 5 |
| 5 |
先阅读然后解答提出的问题:
设a、b是有理数,且满足 ,求ba的值.
,求ba的值.
解:由题意得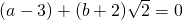 ,因为a、b都是有理数,所以a-3,b+2也是有理数,由于
,因为a、b都是有理数,所以a-3,b+2也是有理数,由于 是无理数,所以a-3=0,b+2=0,所以a=3,b=-2,所以ba=(-2)3=-8.
是无理数,所以a-3=0,b+2=0,所以a=3,b=-2,所以ba=(-2)3=-8.
问题:设x、y都是有理数,且满足 ,求x+y的值.
,求x+y的值.
查看习题详情和答案>>
已知a是方程x2+x-![]() =0的根,求
=0的根,求![]() 的值.
的值.
解:由题意,构造关于a的一元二次方程得a2+a-![]() =0.
=0.
即a2=![]() -a,a2+a=
-a,a2+a=![]() .
.
于是![]() =
=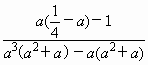
=
=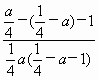
=![]()
=20.
请你构造一个一元二次方程解下列题目:
已知x=-![]() ,求
,求![]() 的值.
的值.
24、阅读下列材料完成后面的问题:
题目:将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
解:在直线y=2x-3上任取两点A(1,-1)、B(0,-3),由题意知,点A向右平移3个单位得A'(4,-1);再向上平移1个单位得A''(4,0),点B向右平移3个单位得B'(3,-3),再向上平移1个单位得B''(3,-2).
设平移后的直线的解析式为y=kx+b,则点A''(4,0)、B''(3,-2)在该直线上,可解得k=2,b=-8,所以平移后的直线的解析式为y=2x-8.
根据以上信息解答下列问题:
将一次函数y=-4x+3的图象向左平移1个单位,再向上平移2个单位,求平移后的直线解析式
查看习题详情和答案>>
题目:将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
解:在直线y=2x-3上任取两点A(1,-1)、B(0,-3),由题意知,点A向右平移3个单位得A'(4,-1);再向上平移1个单位得A''(4,0),点B向右平移3个单位得B'(3,-3),再向上平移1个单位得B''(3,-2).
设平移后的直线的解析式为y=kx+b,则点A''(4,0)、B''(3,-2)在该直线上,可解得k=2,b=-8,所以平移后的直线的解析式为y=2x-8.
根据以上信息解答下列问题:
将一次函数y=-4x+3的图象向左平移1个单位,再向上平移2个单位,求平移后的直线解析式
y=-4x+1
.
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?
小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3-0.5x)元,
由题意得(x+3)(3-0.5x)=10,
化简,整理得:x2-3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系: .
(2)请用一种与小明不相同的方法求解上述问题. 查看习题详情和答案>>
小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3-0.5x)元,
由题意得(x+3)(3-0.5x)=10,
化简,整理得:x2-3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系:
(2)请用一种与小明不相同的方法求解上述问题. 查看习题详情和答案>>