题目内容
先阅读然后解答提出的问题:
设a、b是有理数,且满足a+
b=3-2
,求ba的值.
解:由题意得(a-3)+(b+2)
=0,因为a、b都是有理数,所以a-3,b+2也是有理数,由于
是无理数,所以a-3=0,b+2=0,所以a=3,b=-2,所以ba=(-2)3=-8.
问题:设x、y都是有理数,且满足x2-2y+
y=10+3
,求x+y的值.
设a、b是有理数,且满足a+
| 2 |
| 2 |
解:由题意得(a-3)+(b+2)
| 2 |
| 2 |
问题:设x、y都是有理数,且满足x2-2y+
| 5 |
| 5 |
分析:根据所给信息,先移项,然后将有理数和无理数分组,从而可得(x2-2y-10)+
(y-3)=0,结合所给信息即可得出x、y的值,代入代数式即可得出答案.
| 5 |
解答:解:移项得:(x2-2y-10)+
(y-3)=0,
∵
是无理数,
∴y-3=0,x2-2y-10=0,
解得:y=3,x=±4,
故x+y=7或-1.
| 5 |
∵
| 5 |
∴y-3=0,x2-2y-10=0,
解得:y=3,x=±4,
故x+y=7或-1.
点评:本题考查了实数的运算,解答本题的关键是仔细审题,得到题目所给的解题思路,然后套用这个思路解题,比较新颖.

练习册系列答案
相关题目
 ,求ba的值.
,求ba的值.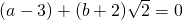 ,因为a、b都是有理数,所以a-3,b+2也是有理数,由于
,因为a、b都是有理数,所以a-3,b+2也是有理数,由于 是无理数,所以a-3=0,b+2=0,所以a=3,b=-2,所以ba=(-2)3=-8.
是无理数,所以a-3=0,b+2=0,所以a=3,b=-2,所以ba=(-2)3=-8. ,求x+y的值.
,求x+y的值.