题目内容
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加1株,平均单株盈利就减少0.5元,要使每盆的盈利达到10元,每盆应该植多少株?小明的解法如下:
解:设每盆花苗增加x株,则每盆花苗有(x+3)株,平均单株盈利为(3-0.5x)元,
由题意得(x+3)(3-0.5x)=10,
化简,整理得:x2-3x+2=0
解这个方程,得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
(1)本题涉及的主要数量有每盆花苗株数,平均单株盈利,每盆花苗的盈利等,请写出两个不同的等量关系:
(2)请用一种与小明不相同的方法求解上述问题.
分析:(1)根据题意可写出平均单株盈利×株数=每盆盈利;平均单株盈利=3-0.5×每盆增加的株数.
(2)除了方程法,可用列表法,图象法和函数法,同学们可选择自己喜欢的方法看看.
(2)除了方程法,可用列表法,图象法和函数法,同学们可选择自己喜欢的方法看看.
解答:解:(1)平均单株盈利×每盆株数=每盆盈利,
平均单株盈利=3-0.5×每盆增加的株数;
(2)解法1(列表法)
答:要使每盆的盈利达到10元,每盆应该植入4株或5株;
解法2(图象法)
如图,纵轴表示平均单株盈利,横轴表示株数,则相应长方形面积表示每盆盈利.
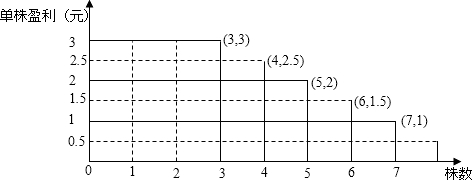
从图象可知,每盆植入4株或5株时,相应长方形面积都是10
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
解法3(函数法)
解:设每盆花苗增加x,每盆的盈利为y元,根据题意得可得:y=(x+3)(3-0.5x),
当y=10时,(x+3)(3-0.5x)=10,
解这个方程得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
解法4(列分式方程)
解:设每盆花苗增加x株时,每盆盈利10元,根据题意,得:
=3-0.5x,
解这个方程得:x1=1,x2=2,
经检验,x1=1,x2=2都是所列方程的解,
答:要使每盆的盈利达到10元,每盆应该植入4或5株.
平均单株盈利=3-0.5×每盆增加的株数;
(2)解法1(列表法)
| 每盆植入株数 | 平均单株盈利(元) | 每盆盈利(元) |
| 3 | 3 | 9 |
| 4 | 2.5 | 10 |
| 5 | 2 | 10 |
| 6 | 1.5 | 9 |
| 7 | 1 | 7 |
解法2(图象法)
如图,纵轴表示平均单株盈利,横轴表示株数,则相应长方形面积表示每盆盈利.

从图象可知,每盆植入4株或5株时,相应长方形面积都是10
答:要使每盆的盈利达到10元,每盆应该植入4株或5株.
解法3(函数法)
解:设每盆花苗增加x,每盆的盈利为y元,根据题意得可得:y=(x+3)(3-0.5x),
当y=10时,(x+3)(3-0.5x)=10,
解这个方程得:x1=1,x2=2,
答:要使每盆的盈利达到10元,每盆应该植入4或5株;
解法4(列分式方程)
解:设每盆花苗增加x株时,每盆盈利10元,根据题意,得:
| 10 |
| x+3 |
解这个方程得:x1=1,x2=2,
经检验,x1=1,x2=2都是所列方程的解,
答:要使每盆的盈利达到10元,每盆应该植入4或5株.
点评:本题考查理解题意的能力,关键能够找到里面的等量关系列出,以及找出和方程不同的方法,如列表法,图象法,函数法等.

练习册系列答案
相关题目