摘要：解:如图9―81.(Ⅰ)作A1D⊥AC.垂足为D.由面A1ACC1⊥面ABC.得A1D⊥面ABC∴∠A1AD为A1A与面ABC所成的角.∵AA1⊥A1C.AA1＝A1C.∴∠A1AD＝45°为所求.(Ⅱ)作DE⊥AB.垂足为E.连A1E.则由A1D⊥面ABC.得A1E⊥AB.∴∠A1ED是面A1ABB1与面ABC所成二面角的平面角.
网址：http://m.1010jiajiao.com/timu_id_425249[举报]
选做题（这里给出了3道选做题，考生只能从中选做一题，多答时按顺序只评第1位置题）A．在极坐标中，圆ρ=2cosθ的圆心的极坐标是
| π |
| 4 |
是
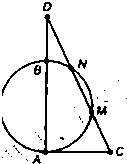
B．如图，AB为⊙O的直径，AC切⊙O于点A，且AC=2
| 2 |
C．若关于x的不等式|x-2|+|x-3|＜a的解集为∅，则α实数的取值范围是
（1）极坐标方程分别为ρ=2cosθ和ρ=sinθ的两个圆的圆心距为
| ||
| 2 |
| ||
| 2 |
（2）如果关于x的不等式|x-3|-|x-4|＜a的解集不是空集，则实数a的取值范围是
a＞-1
a＞-1
；（3）如图，AD是⊙O的切线，AC是⊙O的弦，过C作AD的垂线，垂足为B，CB与⊙O相交于点E，AE平分∠CAB，且AE=2，则AC=
2
| 3 |
2
．| 3 |
请考生在第（1），（2），（3）题中任选一题作答，如果多做，则按所做的第一题记分．（1）选修4-1：几何证明选讲
如图，在△ABC中，D是AC的中点，E是BD的中点，AE的延长线交BC于F．
（Ⅰ）求
| BF |
| FC |
（Ⅱ）若△BEF的面积为S1，四边形CDEF的面积为S2，求S1：S2的值．
（2）选修4-4：坐标系与参数方程
以直角坐标系的原点O为极点，a=
| π |
| 6 |
| π |
| 6 |
（ I）写出直线l的参数方程；
（ II）设l与圆ρ=2相交于两点A、B，求点P到A、B两点的距离之积．
（3）选修4-5：不等式选讲
已知函数f（x）=|2x+1|+|2x-3|．
（I）求不等式f（x）≤6的解集；
（II）若关于x的不等式f（x）＞a恒成立，求实数a的取值范围． 查看习题详情和答案>>
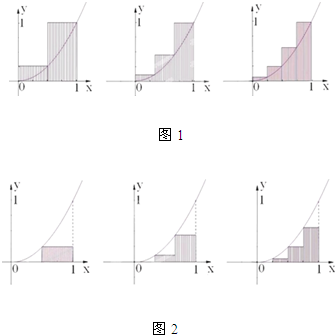为了求函数y=x2，函数x=1，x轴围成的曲边三角形的面积S，古人想出了两种方案求其近似解（如图）：第一次将区间[0，1]二等分，求出阴影部分矩形面积，记为S2；第二次将区间[0，1]三等分，求出阴影部分矩形面积，记为S3；第三次将区间[0，1]四等分，求出S4…依此类推，记图1中Sn=an，图2中Sn=bn，其中n≥2．（1）求a2，a3，a4；
（2）求an的通项公式，并证明an＞
| 1 |
| 3 |
（3）求bn的通项公式，类比第②步，猜想bn的取值范围．并由此推出S的值（只需直接写出bn的范围与S的值，无须证明）．
参考公式：12+22+32+…+(n-1)2+n2=
| 1 |
| 6 |
本题A、B、C三个选答题，请考生任选一题作答，如果多做，则按所做的第一题计分．