题目内容
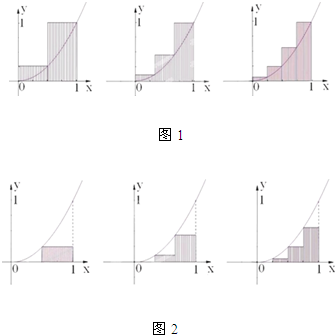 为了求函数y=x2,函数x=1,x轴围成的曲边三角形的面积S,古人想出了两种方案求其近似解(如图):第一次将区间[0,1]二等分,求出阴影部分矩形面积,记为S2;第二次将区间[0,1]三等分,求出阴影部分矩形面积,记为S3;第三次将区间[0,1]四等分,求出S4…依此类推,记图1中Sn=an,图2中Sn=bn,其中n≥2.
为了求函数y=x2,函数x=1,x轴围成的曲边三角形的面积S,古人想出了两种方案求其近似解(如图):第一次将区间[0,1]二等分,求出阴影部分矩形面积,记为S2;第二次将区间[0,1]三等分,求出阴影部分矩形面积,记为S3;第三次将区间[0,1]四等分,求出S4…依此类推,记图1中Sn=an,图2中Sn=bn,其中n≥2.(1)求a2,a3,a4;
(2)求an的通项公式,并证明an>
| 1 |
| 3 |
(3)求bn的通项公式,类比第②步,猜想bn的取值范围.并由此推出S的值(只需直接写出bn的范围与S的值,无须证明).
参考公式:12+22+32+…+(n-1)2+n2=
| 1 |
| 6 |
分析:(1)利用题设条件,根据矩形面积公式,能够求出a2,a3,a4.
(2)仔细观察a2,a3,a4的表示式,能够得到an.再由an=
(n+1)(2n+1)>
×n×2n=
,能够证明证明an>
.
(3)bn=
[(
)2+(
)2+(
)2+…+(
)2]=
[12+22+32+…+(n-1)2]=
(n-1)(n-1+1)(2n-2+1),由此能够推导出bn的取值范围.并由此推出S的值.
(2)仔细观察a2,a3,a4的表示式,能够得到an.再由an=
| 1 |
| 6n2 |
| 1 |
| 6n2 |
| 1 |
| 3 |
| 1 |
| 3 |
(3)bn=
| 1 |
| n |
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n-1 |
| n |
| 1 |
| n3 |
| 1 |
| 6n3 |
解答:解:(1)a2=
[(
)2+12]=
,
a3=
[(
)2+(
)2+12]=
,
a4=
[(
)2+(
)2+(
)2+(
)2]=
.
(2)an=
[(
)2+(
)2+(
)2+…+(
)2+(
)2]
=
[12+22+32+…+(n-1)2+n2]=
(n+1)(2n+1).…(7分)
an=
(n+1)(2n+1)>
×n×2n=
…(9分)
(3)bn=
[(
)2+(
)2+(
)2+…+(
)2]=
[12+22+32+…+(n-1)2]
=
(n-1)(n-1+1)(2n-2+1)
=
(n-1)(2n-1)<
,
∴S=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
a3=
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
| 14 |
| 27 |
a4=
| 1 |
| 4 |
| 1 |
| 4 |
| 2 |
| 4 |
| 3 |
| 4 |
| 4 |
| 4 |
| 15 |
| 32 |
(2)an=
| 1 |
| n |
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n-1 |
| n |
| n |
| n |
=
| 1 |
| n3 |
| 1 |
| 6n2 |
an=
| 1 |
| 6n2 |
| 1 |
| 6n2 |
| 1 |
| 3 |
(3)bn=
| 1 |
| n |
| 1 |
| n |
| 2 |
| n |
| 3 |
| n |
| n-1 |
| n |
| 1 |
| n3 |
=
| 1 |
| 6n3 |
=
| 1 |
| 6n2 |
| 1 |
| 3 |
∴S=
| 1 |
| 3 |
点评:本题考查曲边三角形面积的求法,解题时要认真审题,仔细解答,注意类比推理的合理运用.

练习册系列答案
相关题目
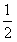 x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元,
x2-200x+80 000,且每处理一吨二氧化碳得到可利用的化工产品价值为100元,