题目内容
 选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)
选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)A.在极坐标中,圆ρ=2cosθ的圆心的极坐标是
| π |
| 4 |
是
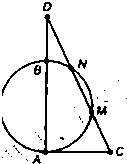
B.如图,AB为⊙O的直径,AC切⊙O于点A,且AC=2
| 2 |
C.若关于x的不等式|x-2|+|x-3|<a的解集为∅,则α实数的取值范围是
分析:A 把极坐标方程化为直角坐标方程,求出交点坐标,再把交点坐标化为极坐标.
B 由圆的切割线定理求得 CM,进而求得 CD,Rt△ACD中,由勾股定理求得AD的值.
C 由|x-2|+|x-3|表示数轴上的x到2和3的距离之和,最小值等于1,可得a的范围.
B 由圆的切割线定理求得 CM,进而求得 CD,Rt△ACD中,由勾股定理求得AD的值.
C 由|x-2|+|x-3|表示数轴上的x到2和3的距离之和,最小值等于1,可得a的范围.
解答:解:A. 圆ρ=2cosθ 的直角坐标方程为 x2+y2=2x,表示圆心为(1,0),半径等于1的圆,
方程θ=
(ρ>0) 即 x-y=0 (x>0),由
得
,
∴交点的坐标为(1,1),∴ρ=
,θ=
,故交点的极坐标为(
,
).
B 由圆的切割线定理得 CA2=CM•CN=CM×(2•CM),∴8=2CM2,CM=2,
∴CD=3•CM=6,Rt△ACD中,AD=
=
=2
.
C∵关于x的不等式|x-2|+|x-3|<a的解集为∅,
|x-2|+|x-3|表示数轴上的x到2和3的距离之和,其最小值等于1,
∴a≤1.
故答案为:A(
,
),B 2
,C (-∞,1].
方程θ=
| π |
| 4 |
|
|
∴交点的坐标为(1,1),∴ρ=
| 2 |
| π |
| 4 |
| 2 |
| π |
| 4 |
B 由圆的切割线定理得 CA2=CM•CN=CM×(2•CM),∴8=2CM2,CM=2,
∴CD=3•CM=6,Rt△ACD中,AD=
| CD2-CA2 |
| 36-8 |
| 7 |
C∵关于x的不等式|x-2|+|x-3|<a的解集为∅,
|x-2|+|x-3|表示数轴上的x到2和3的距离之和,其最小值等于1,
∴a≤1.
故答案为:A(
| 2 |
| π |
| 4 |
| 6 |
点评:本题考查极坐标与直角坐标方程的互化,圆的切割线定理,绝对值的意义,体现了转化的数学思想,绝对值的意义的应用是本题的难点.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
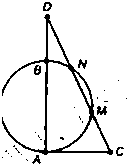 选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)
选做题(这里给出了3道选做题,考生只能从中选做一题,多答时按顺序只评第1位置题)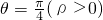 所表示的图形的交点的极坐标
所表示的图形的交点的极坐标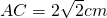 ,过C的割线CMN交AB的延长线于点D,CM=MN=ND,则AD的长等于________cm.
,过C的割线CMN交AB的延长线于点D,CM=MN=ND,则AD的长等于________cm.